中文
Earlier issues
Announcement
More

Progress in Chemistry >

2020 , Vol. 32 >Issue 8: 1203 - 1218

DOI: https://doi.org/10.7536/PC200554

Review

Dynamic Vibrational Spectroscopy in Condensed Matter Chemistry: Theory and Techniques

  • Zhijun Pan 1 ,
  • Wei Zhuang , 1, ** ,
  • Hongfei Wang , 2, 3, **
Expand
  • 1. State Key Laboratory of Structural Chemistry, Fujian Institute of Research on the Structure of Matter, Chinese Academy of Sciences, Fuzhou 350002, China
  • 2. Department of Chemistry and Shanghai Key Laboratory of Molecular Catalysis and Innovative Materials, Fudan University, Shanghai 200438, China
  • 3. School of Science, Westlake University, Hangzhou 310024, China
** e-mail: (Wei Zhuang);
,
(Hongfei Wang)

Received date: 2020-05-09

  Revised date: 2020-05-20

  Online published: 2020-05-25

Supported by

the National Natural Science Foundation of China(21727802)

the National Natural Science Foundation of China(21873101)

Copyright

Copyright reserved © 2020.
Fold

Abstract

The essence of chemical change is the formation and breaking of chemical bonds. The main feature of condensed matter chemistry is that the dynamic interaction and kinetic coupling between the physical and chemical processes in the molecule and the surrounding environment, not only affect the equilibrium and reaction rate of the chemical reaction of chemical bond formation and breaking process, but also change the direction and outcome of the chemical reaction. Dynamic vibration spectroscopy is one of the most powerful modern spectroscopic characterization techniques for detecting various microscopic molecular details in the condensed phase and on its surface or at its interface. Like the pulsed NMR technology, scientists use a set of carefully designed laser pulses to stimulate the complex optical responses in a condensed matter chemical system. The resulting signal contains a much richer information on reaction mechanism than that with traditional absorption spectra. The microscopic information of the molecules such as their structure, molecular motion, charge and energy transfer can be obtained. In recent years, various dynamic vibrational spectroscopy has been developed and applied in various fields of condensed-state chemistry, especially in the field of solution state and surface/interface state. A series of breakthroughs have been made and are in the process of continuous development. In this article, we briefly review and prospect the basic concepts of dynamic vibration spectroscopy techniques, experimental methods and theoretical frameworks, as well as their important applications in condensed state and surface state chemistry.

Contents

1 Introduction

2 Brief description of the experimental techniques

2.1 Two-dimensional coherent infrared spectroscopy

2.2 Interface selective sum-frequency generation vibrational spectroscopy (SFG-VS)

3 Theoretical description of the dynamics of the solution phase vibrational spectroscopy

3.1 SOS (sum over-states) method

3.2 NISE (numerical integration of the Schrödinger equation) method

3.3 NEP (nonlinear exciton propagation) method

3.4 SLE (stochastic Liouville equations) method

4 Two-dimensional infrared technique and its application to solution phase chemistry

5 Sum-frequency generation vibrational spectroscopy technique and its application to surface and interfacial chemistry

6 Conclusions and outlook

Key words： condensed phase chemical dynamics; chemical environmental interaction; dynamic coupling; nonlinear spectroscopy and dynamics; two-dimensional infrared spectroscopy; interfacial vibrational spectroscopy

Cite this article

Zhijun Pan , Wei Zhuang , Hongfei Wang . Dynamic Vibrational Spectroscopy in Condensed Matter Chemistry: Theory and Techniques[J]. Progress in Chemistry, 2020 , 32(8) : 1203 -1218 . DOI: 10.7536/PC200554

1 引言

凝聚态是物质存在的普遍状态之一。凝聚态化学,尤其是关于凝聚态化学的基础理论和实验,是一个广泛的不断发展的研究领域。化学变化的本质是化学键的形成与断裂。现代化学研究最重要的目标,或者圣杯(The Holy Grail),主要包括在理论和实验上对化学键的形成与断裂过程,以及影响它们的热力学和动力学因素的精确认识和细致了解[1],并以此为基础在原子、分子、纳米及介观的层次上对化学反应进行精准控制,以最经济和实用的手段,获得特定结构、性质、功能和数量的化学物质或者器件[2]。如图1a所示,化学科学在能源、材料、环境等所有物质科学与生命科学中起到的中心科学的作用,都离不开对凝聚态化学的基础理论和实验研究,包括凝聚态化学物质的结构、热力学性质和动力学过程的研究,这些研究还具有不可缺少的应用价值。凝聚态化学相关的基础理论和实验研究在中国化学界也越来越得到重视[3,4]。
图1 不同物质状态和化学环境下化学反应及相互热力学关系(Hess循环)

Fig.1 Chemical reactions and thermodynamics under different states and chemical environment(Hess cycle)

人类最早开始认识和利用的化学反应,主要是涉及到凝聚态条件下的复杂化学反应,也就是涉及到液态或者固态的化学反应。人类开始认识和利用简单的化学反应或者在气相中的化学反应,则是在化学知识增长到一定程度之后,逐渐有能力获得纯的化学物质以及对不同成分的气体能够进行分离和提纯之后逐渐进步的。然而,对于化学反应细节的实验和理论研究,却是从最简单的气相基元化学反应开始,逐渐深入到复杂的液相、固相或者异相或者表面反应[5,6]。这既有理论方法上的原因,也有实验技术方面的原因。在理论方面,量子力学计算能够准确处理和计算涉及到三原子的气相基元化学反应,对于超过三原子的气相基元化学反应则需要一定的量子力学或动力学近似处理[5]。在液态中、表面或界面上的化学反应往往是涉及多个步骤的复杂反应,参与化学反应的不同原子、离子或者分子物种处于周围的其他原子、离子或分子的不间断的高频率碰撞和相互作用之中,需要进一步的统计处理,因而理论处理更为复杂。在实验方面,气相基元反应可以通过交叉分子束或激光束等方法,在高真空情况下控制反应物之间的单次碰撞或单次激发条件,研究气相基元反应的能量分配和反应分支等反应细节[5]。对于溶液和表面界面的化学反应,则需要更进一步的实验方法,比如脉冲宽度短于分子碰触碰撞时间过程(一般在皮秒或10-12秒时间尺度)超快激光和其他灵敏的检测手段发展的基础上才能进行。总之,凝聚态,尤其是液态和表面与界面上的化学过程和化学反应的细节理论和实验研究是最近四五十年左右逐渐发展和深入的基础化学理论和实验研究前沿[6,7,8,9]。
控制化学反应的因素,包括热力学因素和动力学因素。从基本热力学的角度来看,在不同的化学环境(气相、液相、固相、异相或表面界面)中发生的涉及到相同的化学键断裂或形成的化学反应,其热力学反应自由能之间的关系可以由图1中的热力学循环关系(Hess循环)联系起来,即:
$\Delta G^{0}_{2} -\Delta G^{0}_{1}=(\Delta G^{0}_{C}+\Delta G^{0}_{D})-(\Delta G^{0}_{A}+\Delta G^{0}_{B}) $
也就是说,反应物与产物分子在不同化学环境下的自由能的差别,等于化学反应的自由能的差别。这个关系很容易地说明为什么反应物和产物在不同化学环境中的能量差别,能够决定在一个化学环境中热力学上能够自发发生的化学反应(反应自由能为负),却可能另外一个化学环境中不能自发发生(反应自由能为负)。这个简单的关系,可以用来分析和比较同一个化学反应在气相、液相、固相和界面上的化学平衡关系,并且根据这些热力学关系认识和了解这些反应的难易程度和如何对特定的化学反应进行热力学调控。
另一方面,传统速率理论的两个基本假设是:(1)能量传递速率远快于化学转化;(2)溶剂能够对溶质变化快速响应从而达到平衡溶剂化。然而当能量传递时间尺度并没有快到能使得能量可以迅速平衡分配到各自由度时,特定能量通路就变得十分重要。另外当溶剂无法迅速对反应做出响应,即时调整时,处于暂态的各个非平衡溶剂化构象对反应会造成不同影响。因此研究化学反应中的动力学因素对我们精确理解和精准控制反应同样非常重要。凝聚态化学过程中的动力学因素较之气态过程更为复杂[6],例如,在气相中的化学反应,原则上只与反应物分子之间的相互碰撞或近距离相互作用或散射过程的细节相关,常常可以进行准确的计算或实验测量[5]。然而,在液相化学反应中,反应物分子并不是孤立的分子,而是被周围的溶剂分子溶剂化,反应物分子之间在液相中的接触或碰撞需要克服溶剂分子的溶剂化作用,因而溶剂分子的特性,如偶极矩、氢键相互作用以及溶剂分子的大小和动态取向等因素,都将影响反应过程中反应物分子之间相互接触的过程,以及产物分子之间相互分开的过程,从而大大影响化学反应发生的动力学过程,或者反应发生的速率[9,10,11,12,13,14]。更进一步,在凝聚态表面或者界面上发生的化学过程和化学反应,由于处于两相之间的分子在表面或界面的不同方向上受到的溶剂和化学环境相互作用不同,不仅在理论上的处理更为复杂,而且会有和体相完全不同的立体化学反应的热力学和动力学效应[7, 15]。复杂的凝聚态化学过程与较为简单气相化学过程之间的最重要的和本质的区别,首先正是在于其化学反应的过程(断键或成键)不再只是反应物分子之间的相互作用所决定,在理论处理和对实验数据进行分析的时候,需要包括所有直接或间接的与溶剂分子相关的短程或长程的相互作用、能量分配和转移的弛豫动力学过程。这些过程在不同的空间尺度和时间尺度上发生,又常常耦合在一起,其耦合程度则取决于不同的分子间相互作用的动态细节[6]。动力学振动光谱技术,是研究凝聚态化学过程中分子机理细节的一类主要工具。各种动力学振动光谱被运用于凝聚态化学的各个领域,尤其是在对时空尺度高度复杂无序的溶液体系中结构,动力学和各类生化过程分子细节的探测中获得了一系列突破性进展。在本文接下来的部分中,我们将主要集中于对水溶液体系体相与界面化学相关动力学振动光谱研究的讨论,以此展示此类技术的基本原理和应用前景。
水普遍存在于自然界中。是生命过程和工业生产中最为常见的溶剂[16]。水分子参与和调控的凝聚态化学反应不仅存在于液相,并且还与表界面上的化学过程密切相关[17,18,19]。水分子的独特结构导致在看似简单的水溶液中和表界面上存在着多尺度并且相互耦合的复杂结构与动力学行为[17,18,20]。对这些动力学行为的精确测定和对其与各种物理、化学及生物过程关联性的理解能帮助我们抽提适用于特定科学问题的溶液图像和理论[16, 20~22]。历史悠久的溶液研究极大地促进了几乎所有主要自然科学领域的进步。然而现有溶液理论囿于所使用的简化假设和图像,在解释伴随新兴科学领域和探测技术涌现的重要溶液现象时经常遇到困难。结合理论和实验理解这些现象的分子图像,完善和发展溶液理论,是当代自然科学中的一个核心课题[6]。例如最新生命科学研究表明细胞内溶液中的许多生物大分子会凝聚形成组分各异的液滴。这些无膜“细胞器”能灵敏地响应溶剂状态和温度等环境变化。这种液-液相分离(liquid-liquid phase separation,LLPS)是众多细胞功能的基础。对LLPS的组分、成因、时空尺度以及细胞液各组分的贡献等基本问题的探索显然能够大大受益于我们对溶液多尺度结构与动力学行为的深刻认识。
当代化学精准化的趋势使得我们越来越需要使用各种表征工具探测溶液体系的分子细节。各种表征工具都被用来对其不同侧面进行研究。动力学振动光谱技术在此有着很好的应用前景。振动光谱直接探测化学键的特征运动和能量,以及能量在分子内和分子间的不同的化学键或振动模式之间的传递和分配的动力学信息。通过对分子体系的多个振动态,或者振动态及电子态的多为激发可以获得丰富的分子运动和反应动力学动态光谱信息。这些信息以及对它们的理论描述能够用来揭示凝聚态中复杂的分子间相互作用、溶剂化现象、和化学键变化及电子运动与化学键变化之间的耦合等现象的机制与机理[23,24,25,26,27,28]。现代的动态振动光谱学技术已成为研究溶液及表面界面化学现象及其相关动力学过程最为有力的工具之一。激光技术的迅猛发展使得研究者们能够在理论上和实验室中使用一组精心设计的脉冲激光序列激发体系中的高阶非线性光学响应,揭示更为丰富的化学体系的动力学信息。因此同时具备良好的时间与结构分辨率的动力学振动光谱理论和技术,已成为研究溶液动力学过程的一类主要实验工具,被逐渐用于探索越来越复杂的溶液体系。例如飞秒红外技术被用来研究细胞液各组分水合动力学(hydration dynamics)以及生物分子构象涨落,其结果显示水合动力学几乎不受细胞膜等因素限制,是细胞液的内禀属性。因此可以直接研究溶液分子的光谱动力学响应来获得许多有用的细胞内分子动力学信息[28]。
前沿的光脉冲技术能够改变光波包络、偏振方向、持续时间和时间延迟、调谐频率以及控制光脉冲的相位,使得大量发展于核磁共振领域中的概念、方法与技术能够扩展到光学领域。仔细设计的激光脉冲序列能够在特定方向上缩减谱峰线宽来改善光谱分辨率,增强特征峰的强度,进行各种锁相外差技术的相干叠加,以及进行偏振敏感的测量。通过将信号显示为各种时间延迟的相关图,这些谱学信号能够表现各种微观动力学的详细信息,例如聚集体的协同运动或肽键的振动[22,29~31]。多维光谱技术还可以通过一次测量实时探测振动弛豫完整路径和构象涨落。泵浦-探测(pump-probe)、荧光退偏振(fluorescence depolarization)、光子回波(photon-echo)、烧孔(hole-burning)和荧光干涉术(fluorescence interferometry)等信号能够直接测量分子体系中的激发态布居转移和弛豫。光子回波技术可以选择性消除两能级系统的静态非均匀展宽等。由于体系的复杂性,实验光谱信号很难被深入地直接解读,高水平的光谱理论计算因此在本领域中扮演着不可或缺的重要角色。动力学光谱模拟需要求解多自由度体系与光场耦合的运动方程,是理论与计算化学中非常重要并具有挑战性的课题[23,25,26,28]。
在凝聚态化学研究中,与液体有关的体相或异相(表面与界面)过程,由于其高度的动态结构和相互作用的特征,是现代凝聚态化学理论和实验研究的前沿。现代先进光谱动力学理论和实验方法是研究化学键变化,能量分配和电荷转移,以及溶剂化效应和各种时间、空间和量子态耦合的基本研究方法,并且在不断发展之中。在本文中我们将回顾非线性动力学振动光谱技术,包括二维相干红外光谱(2D IR即two-dimensional infrared spectroscopy)[23, 25,26, 32]和界面和频振动光谱(SFG-VS, 即sum-frequency generation vibrational spectroscopy) [33,34,35,36]的基本概念、实验方法和理论框架,以及它们在溶液态化学和表面界面化学中的重要应用[28]。

2 实验方法简介

在过去的二十多年来,2D IR和SFG-VS的理论和技术得到了系统的发展,在研究溶液和表面界面的光谱与动力学方面得到了越来越广泛的应用。这里只对其中比较常用的基本技术作简要介绍,更多的信息可参考相关的专著及综述文献[23,25,26,33,34]。

2.1 二维相干红外光谱

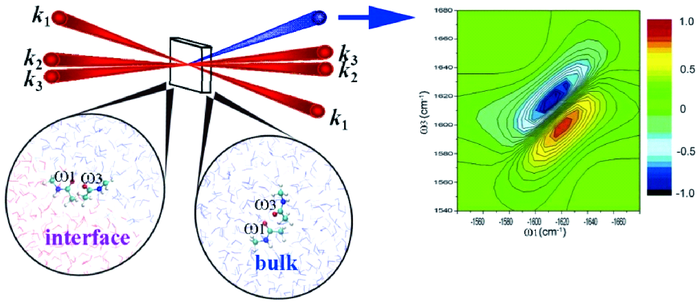
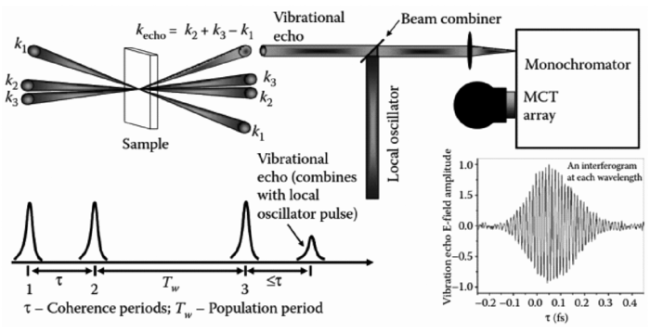
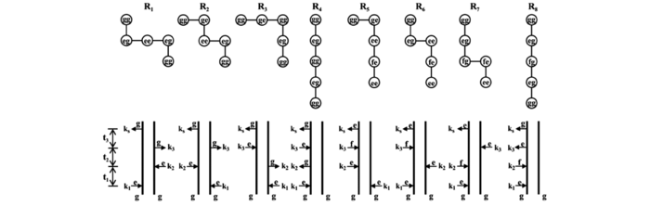
二位相干红外光谱实验是将一组精心设计的激光脉冲序列施加于样品体系,并由此激发起复杂的光学响应[23]。所产生的相干非线性信号中包含了比传统吸收光谱丰富得多的反应机理、分子与溶液结构、分子运动、电荷与能量传递等微观信息[1,2,3]。与线性的FTIR光谱将体系分子信息投影到单一的时间或者频率维度不同,近年来备受关注的二维相干红外光谱提供了多维度的图像[23]。
在典型和常用的外差式探测(heterodyne-detected)二维相干红外光谱实验中,体系与外加光场三次相互作用(外场波矢分别为 k 1 , k 2 , k 3 )后,在 k s = ± k 1 ± k 2 ± k 3 的方向上产生相干信号 S ( t ) , 并由在同一波矢方向的第四束光场探测得到(图2)[37]。信号 S ( t ) 是探测光场与试样相互作用前后的强度差,并与四次光场-试样相互作用之间的时间间隔t3,t2,t1相关。二维红外光谱通过将 S ( t ) 三个时间参数中的某一个(例如 t 2 )固定,而以另外两个时间轴展开来获得。这样的二维图通常看起来高度振荡。为了获得更为清晰的图像,通常将 t 1 和 t 3 做双重傅里叶变换来生成 S ( Ω 3 , t 2 , Ω 1 ) 的二维频率图谱(图2)。相互耦合的振动模式在单振荡模式的加和频率上产生新的共振。这些交叉峰的强度和线型反映了振动跃迁之间的关联。 S ( t ) 可以表达为多点关联函数,因此包含了比线性信号对应的两点关联函数丰富的多的信息。
图2 外差式探测(heterodyne-detected)的二维相干红外光谱实验示意图(左): 三个时间延迟t1, t2, t3 保持第三个时间延迟固定,并在涉及两个时间延迟的演化得到二维相关信号图。(右上): 沿相位匹配方向; $k_{I}=k_{1}+k_{2}+k_{3}$的两个耦合振动的二维光子回波谱。 ω1 和ω3是t1 和t3的傅里叶共轭物理量。 两种振动模式的频率涨落分别是慢速和反相关(左),慢速和相关(中),快速和反相关(右)。(右下):三个模型对应的线性吸收光谱

Fig.2 (left) Pulse configuration for a heterodyne detected multidimensional four-wave mixing experiment. Signals are recorded versus the three time delays t1, t2, t3, and displayed as 2D correlation plots involving two of the time delays, holding the third time delay fixed;(right top): 2D photon-echo spectra of two coupled vibrations in the phase-matching direction $k_{I}=k_{1}+k_{2}+k_{3}$. ω1 and ω3are the Fourier conjugate variables to t1 and t3. The frequency fluctuations of the two modes are slow and anti-correlated(left panel), slow and correlated(middle panel), fast and anti-correlated(right panel).(Right bottom): Linear absorptions for the three models

图3是二维相干红外光谱的实验脉冲序列的示意图[28]。实验中一般是通过钛蓝宝石(Ti: sapphire)固体再生放大器泵浦光参量放大器(OPA)产生三个激励脉冲,其持续时间约为60 fs。脉冲序列显示在图的底部。将OPA调整为正在研究的振动模式的频率。IR脉冲具有足够的带宽以跨越感兴趣的光谱区域。脉冲1和2之间以及脉冲2和3之间的时间分别称为τ和Tw。振动回波信号在第三个脉冲后的唯一时间≤τ处从样本辐射出来。通过以固定的Tw扫描τ记录振动回波信号。信号在空间和时间上与用于外差检测的本地振荡器重叠,并且组合的脉冲被单色仪分散到IR阵列检测器上。外差探测可提供幅度和相位信息。如果在从样品中出现时检测到振动回波,则没有相位信息。实验会在频域中产生二维频谱。在时域中进行测量。从时域到频域需要两个傅里叶变换。要执行傅里叶变换,需要振幅和相位信息。本地振荡器是另一个红外飞秒脉冲,该脉冲来自相同的初始脉冲,该初始脉冲被分割成激励脉冲。当它与振动回波包重叠时,会发生干扰。随着时间τ的扫描,振动回波波包电场在固定的本地振荡器波包电场上随时间移动结果为具有必要相位信息的时间干涉图。时间干涉图的一个示例显示在图3的右下部分。
图3 二维红外振动回波实验示意图及振动回波脉冲序列和时间干涉图示例,这是外差检测到的结果振动回波技术[28]

Fig.3 Schematic diagram of two-dimensional infrared vibrational echo experiment. An example of vibrational echo pulse sequence and time interferogram is also shown, which is the result of heterodyne detection[28]

2.2 界面和频振动光谱(SFG-VS)

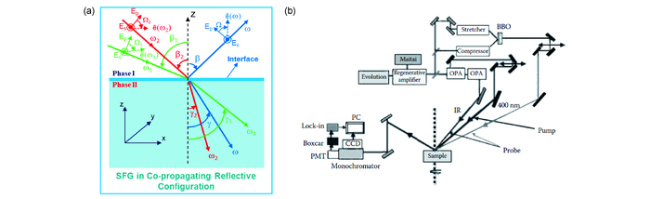
和频振动光谱(sum-frequency generation vibrational spectroscopy, SFG-VS)是测量表面和界面的原子、分子与电子结构与相互作用的二阶非线性光学方法[33]。界面二阶非线性光学方法包括光学二次谐波(optical second harmonic generation, SHG)与和频振动光谱。1980年代初,美国加州大学Berkeley分校物理系的沈元壤等率先发展了界面SHG 和SFG-VS方法用于系统地研究分子的表面和界面现象。SHG和SFG都是在激光与分子相互作用过程中,由两个光子合并产生一个频率为二者频率加和的新的光子的过程。当两个光子频率和来源相同时,这一过程被称为光学二次谐波。频率不同时,则被称为和频过程。二阶非线性光学过程的一个基本特征,是这一过程在具有完全中心对称性结构的分子或者宏观体系其响应强度几乎可以忽略不计,因而成为选择性测量在非对称的相互作用条件下的总是具有非中心对称结构的表面和界面上的分子的有效方法。随着激光技术和微弱信号检测技术的发展,SFG-VS可以对亚单分子层覆盖的表面或界面进行选择性的灵敏测量。
图4分别是用于研究表面和界面的光谱与动力学的SFG-VS的基本原理图(图4a),和用于获得时间分辨的和频振动光谱的典型实验装置图(图4b)[28]。
图4 (a)和频振动光谱基本原理示意图[35]。(b)时间分辨SFG实验中使用的实验装置示意图。设置用于研究表面及界面的过程的超快光谱和界面分子结构,及溶剂化、相互作用、能量和电子转移动力学等。其中泵浦光(pump)可以沿表面法线入射,也可以由其他角度入射[28]

Fig.4 (a) Basic principle of sum-frequency generation vibrational spectroscopy[35]; (b) Schematic diagram of experimental device used in time-resolved SFG experiment. The experimental device is configured to study ultrafast spectrum and molecular structure of the interface, solvation, interaction, energy and electron transfer dynamics, etc. of the surface and interface processes. The pump can be incident along the normal of the surface or other angles[28]

如图4a所示,在和频振动光谱的测量中,常用一个固定频率的可见光和波长可以变化的红外激光与表面或界面相互作用,并检测随红外波长变化的光谱信号,获得和频振动光谱。因为和频振动光谱能够直接测量界面上不同的分子基团的振动光谱,以分析界面上分子基团的密度与密度变化、取向与取向变化,从而可以获得表面和界面上分子的结构、构象与相互作用过程的信息。和频振动光谱的定量分析,需要对入射的红外和可见光,以及出射的和频信号光的入射与出射角(βi),偏振角(Ωi)的组合进行和频光谱的准确测量。这些定量测量和分析方法都已经被系统地发展出来了[17,38]。和频振动光谱能够测量不同化学基团振动光谱的化学选择特定性使其很快成为研究化学、材料、能源、环境和生命科学中重要的表面和界面问题的最重要的工具[7,8, 28,33~36, 39,40]。SFG-VS在过去三十多年中已经取得了很多重要的研究结果,在研究技术方面也得到了不断的发展。通过选择红外或者可见光的频率,可以实现不同类型的和频振动或者电子光谱,用于研究电子基态上的振动态,电子激发态上的振动态,以及电子激发态的信息与分子过程。在研究技术方面,SFG-VS从一开始固定可见光波长,并使用波长扫描的纳秒红外激光,再到使用波长扫描的皮秒红外激光,再到使用不许扫描的宽带的红外激光,在光谱分辨率和时间分辨率、信号强度、相位检测方法上都有不断的进步[36, 41~44]。在和频振动光谱的定量测量和光谱分析方法发展的同时,和频振动光谱也可以用来测量表面和界面上的分子光谱和动力学过程[7,8]。
图4b是一个典型的时间分辨的和频振动光谱测量装置图[28]。这里一束宽带飞秒红外光和一束窄带的皮秒可见光被用来作为SFG-VS的检测光(probe),另一束400 nm(也可以是从紫外到可见和红外的其他波长)的飞秒激光作为泵浦光(pump),通过泵浦光与检测光的时间延迟对检测的界面SFG信号的影响,就可以测量时间分辨的和频振动光谱,获得界面分子的时间分辨的动力学信息。与前面介绍的实现分辨二维红外相干光谱类似,SFG-VS也可通过对激光脉冲的选择和设计,进行所谓二维和频振动光谱(2D-SFG-VS)的测量。类似于二位红外光谱的2D-SFG-VS的理论描述和模拟方法,也在过去十年中发展起来并应用于表面和界面的光谱动力学测量[23, 45~48]。由于SFG-VS是能够对各类表面和界面进行灵敏的选择性测量的实验方法,2D-SFG-VS光谱动力学研究是表面和界面非线性光谱动力学研究的前沿,还有待进一步的发展和应用。

3 溶液相振动光谱的动力学理论描述

溶液相中分子的光谱与动力学理论描述经过系统的发展已经比较成熟。通过这些描述,分子的电子与振动状态及相互作用,以及与溶剂分子的耦合参数等能够直接跟不同的光谱和动力学实验的测量方法和结果联系起来,从而通过理论和计算模拟结果与实验结果进行比较,进而获得溶液相中分子的光谱与动力学阐述[6, 25,26, 32, 49]。这里的描述是基于典型的二维红外光谱测量展开的,与二维红外类似的二维SFG-VS光谱动力学具体理论描述也可以类似地发展出来[28, 45,46, 50]。
非线性光谱动力学测量中的光谱信号可以很自然地通过它们对驱动光场的幂定律依赖性来分类。例如体系与光场作用n+1次(包括探测光场)的外差(heterodyne)测量实验[32]:
E υ = ∑ j = 1 n [ E ~ υj ( t - t j ) exp ( i k j · r - i ω j ( t - t j ) + i ϕ j ) + E ~ υj * ( t - t j ) exp ( - i k j · r + i ω j ( t - t j ) - i ϕ j ) ]
其中 E ˙ υj (t-tj)是以tj为中心的脉冲光场j的轮廓,而kj,ωj和φj则是其波矢,频率和位相。光谱信号S(t;t3,t2,t1)通过求解Maxwell-Liouville方程可以写成[32]:
S(t) ∝ Im [ E ˙ υ 4 * (t) P ( n ) ( k s , t ) ]
其中的P(n)(ks,t)是体系n阶极化度:[32]
P ( n ) ( k s , t ) = ∫ dr P υ 4 ( n ) ( r , t ) exp ( ⁃ i k s · r + i ω s t )
P υ 4 ( n ) (r,t)可以写成响应方程与外加光脉冲序列的光电场卷积的形式。
P υ 4 ( n ) ( r , t ) = ∫ 0 ∞ d t n ∫ 0 ∞ d t n - 1 … ∫ 0 ∞ d t 1 S ( n ) ( t n , t n - 1 , … , t 1 ) × E ( r , t - t n ) E ( r , t - t n - t n - 1 ) … E ( r , t - t n - t n - 1 … - t 1 )
光响应方程是包含了所有相关分子信息的体系性质张量。例如对于常用的四波混频信号[37],
P ν 4 ( 3 ) ( r , t ) = ∑ ν 3 ν 2 ν 1 ∫ 0 ∞ d t 3 ∫ 0 ∞ d t 2 ∫ 0 ∞ d t 1 S ν 4 ν 3 ν 2 ν 1 3 ( t 3 , t 2 , t 1 ) E ν 3 ( r , t - t 3 ) E ν 2 ( r , t - t 2 - t 3 ) E ν 1 ( r , t - t 1 - t 2 - t 3 )
其对应的是三阶光响应方程[37]:
$S^{(3)}_{\nu4\nu3\nu2\nu1}(\tau4,\tau3,\tau2,\tau1)=(\frac{1}{h})^3<\Bigg{[}\Big{[}[v_{\nu4}(\tau4), v_{\nu3}(\tau3)], v_{\nu2}(\tau2)\Big{]},v_{\nu1}(\tau1)\Bigg{]}>$
响应方程中的嵌套对易子展开后,可以写成多条刘维尔(Liouville)空间路径的加和(图5) [32]。对共振信号的主要贡献仅来自于电场和分子振动频率有相反的符号的部分。可以安全地忽略其他(相同符号)高频振荡的部分(旋波近似,RWA,即rotating wave approximation)。每个相位匹配的信号由Liouville空间路径的特定组合来描述,具体取决于激光的脉冲序列设置和探测模式。由于对称性,奇数阶响应发生在体相,偶数阶响应则发生在界面。
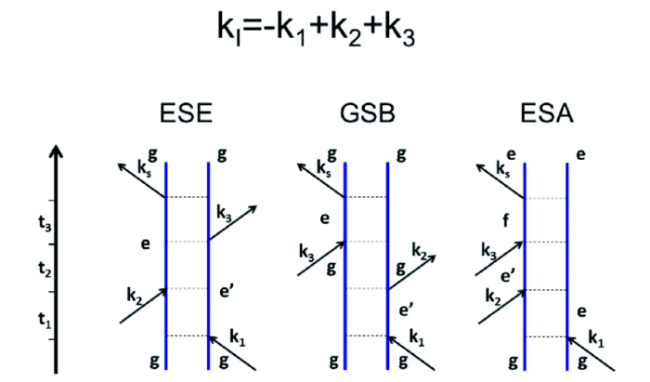
图5 常见的八条刘维尔空间路径(上)及其对应费曼图(下),每条刘维尔空间路径从左上的圆开始,而费曼图从底部开始演化[51]

Fig.5 Eight Liouville-space pathways(upper) and double-sided Feynman diagrams(lower) for two-dimensional spectroscopy in the rotating wave approximation. Each Liouville-space pathway starts from the upper-left circle, while the double-sided Feynman diagram starts from the bottom[51]

通常用来计算动力学振动光谱的非线性响应函数模拟方法,包括最常用的各态加和法(sum-over-states, SOS)[23,25,27,32,37,49,52,53]结合高斯涨落的累积展开法(cumulant expansion of Gaussian fluctuation, CGF)的方法,以及如随机Liouville方程(stochastic Liouville equation, SLE)[54]和Schrödinger方程的数值积分(numerical integration of the Schrödinger equation, NISE)[55,56]等数值演化方法。

3.1 SOS(sum over-states)方法

作为模拟和分析非线性响应函数的最常用理论方法,各态加和方法需要计算所有的第一激发和第二激发跃迁并将其加和,将响应方程重塑为关联函数的组合,并假设哈密顿量具有高斯涨落,通过cumulant expansion等处理来计算信号。例如,通过具有相位匹配条件kI=-k1 + k2 + k3的脉冲序列创建重相信号 S K I ,其中在共轭相位的t1和t3期间会产生相干性。该信号由三个途径贡献[52]:
S ν 4 ν 3 ν 2 ν 1 K I τ 4 , τ 3 , τ 2 , τ 1 = i ħ 3 ∑ n 1 n 2 n 3 n 4 μ n 1 ; ν 1 (τ1) μ n 2 ; ν 2 (τ2) μ n 3 ; ν 3 (τ3) μ n 4 ; ν 4 (τ4)×(<g| B n 1 U τ 1 , τ 2 B n 2 † U τ 2 , τ 4 B n 4 U τ 4 , τ 3 B n 3 † |g>+<g| B n 1 U τ 1 , τ 3 B n 3 † U τ 3 , τ 4 B n 4 U τ 4 , τ 2 B n 2 † |g>-<g| B n 1 U τ 1 , τ 4 B n 4 U τ 4 , τ 3 B n 3 † U τ 3 , τ 2 B n 2 † |g>)
振动的时间演化算符U τ 2 , τ 1 表示为[32:
U τ 2 , τ 1 = ex p + - i ħ ∫ τ 1 τ 2 H ( τ ) dτ
其中exp+表示时间顺序的指数运算符。公式(8)中的三个项分别对应于基态漂白(GSB),激发态吸收(ESA)和激发态发射(ESE)的贡献[37]。
S GSB K I t 3 , t 2 , t 1 =- i ħ 3 <μge τ 1 Uee τ 1 , τ 2 μeg τ 2 μge τ 4 Uee τ 4 , τ 3 μeg τ 3 >ΓGSB(t3,t2,t1)
S ESE K I t 3 , t 2 , t 1 =- i ħ 3 <μge τ 1 Uee τ 1 , τ 3 μeg τ 3 μge τ 4 Uee τ 4 , τ 2 μeg τ 2 >ΓESE(t3,t2,t1)
S ESA K I t 3 , t 2 , t 1 =- i ħ 3 <μge τ 1 Uee τ 1 , τ 4 μef τ 4 U ff τ 4 , τ 3 μ fe τ 3 U ee τ 3 , τ 2 μeg τ 2 >ΓESA(t3,t2,t1)
其中τ1,τ2,τ3,τ4是系统与外部电场进行相互作用的时间。振动寿命由弛豫因子来描述:[37]
ΓGSB t 3 , t 2 , t 1 =exp(- t 3 + 2 t 2 + t 1 /2T1)
ΓESE t 3 , t 2 , t 1 =exp(- t 3 + 2 t 2 + t 1 /2T1)
ΓESA t 3 , t 2 , t 1 =exp(- t 3 + 2 t 2 + t 1 2 T 1 - t 3 2 T 2 )
T1,T2分别是单激发态和双激发态的寿命。
图6显示了在每个时间间隔内密度矩阵状态下kI技术的不同费曼图的三个贡献[32]。体系能级由三个良好分离的能带组成,如图6所示,g为基态,e为第一激发态多重态,f为第二激发态多重态。脉冲可引起的跃迁为μge和μef。仅允许基态g与第一激发态多重态e之间以及第一与第二激发态多重态f之间的跃迁。可以通过对振动本征态之间所有可能的跃迁求和(因此称为sum-over-states)来计算响应函数。非线性响应对于谐波振动消失,因此可以归因于非谐性。
图6 表示在旋转波近似中有助于kI信号的Liouville空间路径的费曼图。这三种途径被称为激发态发射(ESE),基态漂白(GSB)和激发态吸收(ESA)

Fig.6 Feynman diagram representing the Liouville space path for the kI signal in the rotating wave approximation where these three pathways are called excited state emission(ESE), ground state bleaching(GSB), and excited state absorption(ESA)[32]

如果所有状态的频率涨落都服从高斯统计,则可以使用高斯涨落的累积扩展(CGF)来计算响应函数。引入Δωma(t) ≡ ωma(t)- ω ̅ ma 来表示跃迁频率的涨落,其中 ω α ̅ β 是平均跃迁频率。Δω的二次相关函数为[32]:
Cmn ( τ 1 , τ 2 )= 1 ħ 2 <Δωma(τ1)Δωna(τ2)>≡C' t 1 +iC″ t 1
其中C'(t)和C″(t)是C的实部和虚部,t1=τ1- τ2表示时间间隔。线宽函数可以定义为[32]:
g mn ( t ) = ∫ 0 t d τ 2 ∫ 0 τ 1 d τ 2 C mn τ 2 )
利用C' 与 C″间的涨落耗散关系,gmn(t)可表示为[32]:
g mn ( t ) = ∫ - ∞ ∞ dω 2 π 1 - cos ωt ω 2 coth ħ ω 2 k B T C ″ mn ω + i ∫ - ∞ ∞ dω 2 π sin ωt - ωt ω 2 C ″ mn ( ω )
其中
C ″ mn ( ω ) = 2 ∫ 0 ∞ d sin ωt C ″ mn t
为谱密度函数。gnm(t)的实部和虚部分别代表光谱的展宽和移位。三阶非线性响应函数可以用g(t)表示。
CGF方法仅描述能量的对角线涨落,而无法描述非对角线耦合和跃迁偶极矩的涨落。它也不计入涨落的非高斯部分。此外,CGF使用固定的激子,而忽略了本征态涨落。因此难以处理高度无序的溶液体系。另一方面,由于中心极限定理,CGF方法应适用于更广泛的系统,在这些系统中,集体坐标可以表示为许多热库坐标之和,而贡献很小。例如,当集体坐标是某个位置处的电场时,由环境中所有电荷的贡献之和得出。再进而采用Condon近似忽略与跃迁偶极子一样大的涨落。对于具有可分为多个时间段的动力学的系统,我们可以采用非均匀CGF方案,并通过对缓慢互变构型的贡献进行求和来计算频谱,每个互变构型由CGF计算。

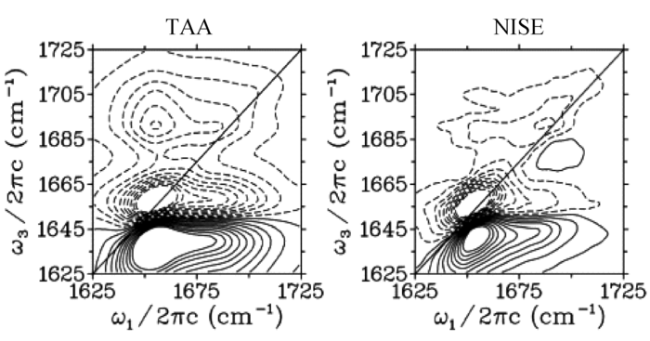
3.2 NISE(numerical integration of the Schrödinger equation)方法

非线性响应函数也可以通过对薛定谔方程进行数值积分(NISE)来计算。NISE方法能够考虑到非绝热效应。对于n激子波函数,随时间变化的薛定谔方程表示为[57]:
iħ ∂ ∂ t | ψ ν 1 ( n ) t ; τ 1 >=H(t)|ψ(n ) ν 1 t ; τ 1 >
考虑的激发态多重态可以根据的原基函数|φ>来构建波函数[57]:
| ψ i ( n ) t ; τ 2 ; τ 1 > = ∑ j c ij t ; τ 2 ; τ 1 | φ j ( n ) >
对于t=0,展开系数满足cji(0)=δji。将方程(21)代入与含时间的Schrödinger方程(20)中,即可得到展开系数方程[57]:
iħ ∂ ∂ t c ij ( t ) = ∑ k H ik ( t ) c jk t
把∂t改为Δt,在持续时间Δt的这样一个时间步长上的数值积分得出[57]:
c ij ( ( n + 1 ) Δt ) = exp - i ħ ∑ k H ik nΔt Δt c jk nΔt ≡ ∑ k U ik ( n + 1 ) Δt , nΔt c jk nΔt
其中,时间演化算符U ( n + 1 ) Δt , nΔt 将时间相关系数从时间nΔt传播到(n + 1)Δt。因为使用较小的时间增量对该方程进行数值积分,所以每个积分步骤中可以将哈密顿量视为常量。然后,方程(9)中的传播子可以写成普通指数因子的乘积[57]:
U nΔt , 0 = ex p + - i ħ ∫ 0 nΔt H ( τ ) dτ
哈密顿量Hik nΔt 通常随时间变化,因此对响应函数进行数值积分的收敛可能会非常耗时。有一种方法叫做时间平均近似(time-averaging approximation, TAA)克服这些问题[58,59]。通过在一些适当选择的固定时间T上平均的频率,可以得出一种线形的近似表达式,该表达式涉及替换在时间t上平均的上述频率。方程中振动时间演化算子U τ 2 , τ 1 变成了[58,59]:
U t , 0 = ex p T - it ħ 1 t ∫ 0 t H ( τ ) dτ ≈ ex p T - it ħ 1 t ∫ 0 t ω ( t ' ) dt '
ω T = 1 T ∫ 0 T ω ( t ' ) dt '
然后,传播仅涉及平均频率ωT。这个表达式由Auer和Skinner使用固定时间间隔T上的平均值近似提出。TAA以非常有效的方式加速了数值过程,考虑了线性吸收光谱中的动态影响。Jansen和Ruszel使用了稍微更一般的表达式,引入了权重函数,例如指数函数,盒形函数或高斯函数[59]。
ω τ A EXP = 1 τ A ∫ t ∞ e ( - ( t ' ⁃ t ) / τ A ) ω ( t ' ) dt '
ω τ A BOX = 1 τ A ∫ t t + τ A ω ( t ' ) dt '
ω τ A GAUSS = 2 2 π 　 τ A ∫ t ∞ e xp - 1 2 ( t ' ⁃ t τ A ) ω ( t' ) d t'
在非常广阔的时间尺度范围内,高斯权函数对于常见的过度阻尼布朗模型给出了最佳结果。对于孤立的生色团Kubo模型,只要选择的平均时间不在极窄范围内,该时间平均近似就可以使用。对于具有许多相互作用的生色团的复杂问题,此方法的功能尤其明显。
图7显示了与NISE光谱相比在垂直极化配置下的TAA光谱[55]。使用高斯加权函数的167 fs平均时间,通过时间平均过程计算左频谱。这对应于20 cm-1的不均匀线宽。TAA重现了光谱的基本结构。但是,这些峰通常太宽,在TAA计算中(ω1,ω1)=(1650 cm-1,1690 cm-1)处的交叉峰太强。这些差异可能是由于在时间延迟t1和t3期间忽略了非绝热效应,也可能是由于哈密顿量的所有元素均以相同的平均时间求平均而引起的。后者对于波动联轴器可能是一个特殊的问题。通过优化平均过程以解决耦合涨落的问题,有可能改善一致性。在用于Trpzip2模拟的同一台计算机上,NISE计算花费了100 h,而TAA计算花费了不到1 min。
图7 在TAA中使用Jansen和Ruszel的NISE计算的β-发夹Trpzip2的酰胺I带的2DIR光谱

Fig.7 The 2DIR spectrum of the amide I region for β-hairpin Trpzip2 calculated in the TAA and using the NISE.[59]

3.3 NEP(nonlinear exciton propagation)方法

非线性响应函数还可以通过激子模型的数值积分(nonlinear exciton propagation)来计算[37]:
$S^{(3)}_{\nu4\nu3\nu2\nu1}(\tau4,\tau3,\tau2,\tau1)=(\frac{1}{h})^3<\Bigg{[}\Big{[}[v_{\nu4}(\tau4), v_{\nu3}(\tau3)], v_{\nu2}(\tau2)\Big{]},v_{\nu1}(\tau1)\Bigg{]}>$
其中 ν i 为笛卡尔坐标系下极化方向(xyz),可以从响应函数方程中的三个嵌套对易子推导出8个Liouville空间路径。这些路径组成了各种非线性响应函数子类。如光子回波信号可表示为[37]:
S ν 4 ν 3 ν 2 ν 1 K I (τ4,τ3,τ2,τ1)= i ħ 3 ∑ n 1 n 2 n 3 n 4 μ n 1 ; ν 1 (τ1) μ n 2 ; ν 2 (τ2) μ n 3 ; ν 3 (τ3) μ n 4 ; ν 4 (τ4)×(<g| B n 1 U(τ1,τ2) B n 2 † U(τ2,τ4) B n 4 U(τ4,τ3) B n 3 † |g>+<g| B n 1 U(τ1,τ3) B n 3 † U(τ3,τ4) B n 4 U(τ4,τ2) B n 2 † |g>-<g| B n 1 U(τ1,τ4) B n 4 U(τ4,τ3) B n 3 † U(τ3,τ2) B n 2 † |g>)
通过引入单激子和双激子格林函数,公式(9)中的时间演化算符表示为[37]:
G n 2 , n 1 (τ2,τ1)=<g| B n 2 U(τ2,τ1) B n 1 † |g>
G n 2 m 2 , n 1 m 1 (τ2,τ1)=<g B n 2 B m 2 U ( τ 2 , τ 1 ) B n 1 † B m 1 g>
最终,公式(31) 化简为[37]:
S ν 4 ν 3 ν 2 ν 1 K I ( τ 4 , τ 3 , τ 2 , τ 1 ) = 2 i ħ 4 ∑ n 1 n 2 n 3 n 4 　 ∑ m 1 m 2 m 3 m 4 p 2 μ n 1 ; ν 1 ( τ 1 ) μ n 2 ; ν 2 ( τ 2 ) μ n 3 ; ν 3 ( τ 3 ) μ n 4 ; ν 4 ( τ 4 ) × ∫ τ 3 τ 4 d G n 4 m 4 ( τ 4 , s ) U m 4 m 1 m 3 m 2 ( s ) G m 3 m 2 , n 3 p 2 ( s , τ 3 ) G p 2 n 2 ( τ 3 , τ 2 ) G m 1 , n 1 * ( s , τ 1 )
非线性响应表示为与k3和k4脉冲相互作用之间的时间间隔s的时间积分。说明了等式中谐波部分的精确抵消。并且这些方程现在受到非谐性Uijlk显式影响到一阶,但是高阶通过 G ( s , τ 3 ) 。 为了提高计算效率,方程式中的格林函数,它不是直接计算的,而是引入了一个激子和两个激子的时变波函数,表示如下[37]
ψ m 1 ; υ 1 ( 1 ) ( s ; τ 1 ) = ∑ n 1 G m 1 , n 1 ( s , τ 1 ) μ n 1 ; ν 1 ( τ 1 )
ψ m 1 m 2 ; υ 1 ; υ 2 ( 2 ) ( s ; τ 2 ; τ 1 ) = ∑ n 1 G m 2 m 1 , n 2 n 1 ( s , τ 2 ) μ n 2 ; ν 2 ( τ 2 ) ψ n 1 ; υ 1 ( 1 ) ( τ 2 ; τ 1 )
方程(35)中 ψ m 1 ; υ 1 ( 1 ) (s;τ1)的描述了在时间τ1处通过跃迁偶极子 μ n 1 ; ν 1 (τ1)相互作用产生的单个激子的演化。引入 ψ m 1 m 2 ; υ 1 ; υ 2 ( 2 ) (s;τ2;τ1)来表示双激子传播。在时间演化过程中,第一个激子在时间τ1处创建,并作为第二个激子传播到时间τ2,然后传播到时间s。当起始时间设为s=τ2,由单激波函数 ψ m ; υ 1 ( 1 ) (s;τ1)结合跃迁偶极子 μ m ; ν 2 (τ2)生成的对称乘积给出了两激子波函数[37]:
ψ m 1 m 2 ; υ 1 ; υ 2 ( 2 ) (τ2;τ2;τ1)= ψ m 1 ; υ 1 ( 1 ) (τ2;τ1) μ m 2 ; ν 2 (τ2)+ ψ m 2 ; υ 1 ( 1 ) (τ2;τ1) μ m 1 ; ν 2 (τ2)
使用以下定义,等式(30)可以进一步改组[37]:
S ν 4 ν 3 ν 2 ν 1 K I ( τ 4 , τ 3 , τ 2 , τ 1 ) = 2 ( i ħ ) 4 ∑ n 4 μ n 4 ; ν 4 ( τ 4 ) R n 4 ; ν 3 ν 2 ν 1 K I ( τ 4 , τ 3 , τ 2 , τ 1 )
R n 4 ; ν 3 ν 2 ν 1 K I ( τ 4 , τ 3 , τ 2 , τ 1 ) = ∑ m 4 ∫ τ 3 τ 4 d G n 4 m 4 ( τ 4 , s ) X m 4 ; ν 3 ν 2 ν 1 K I ( s ; τ 3 , τ 2 , τ 1 )
X m 4 ; ν 3 ν 2 ν 1 K I ( s ; τ 3 , τ 2 , τ 1 ) = ∑ m 1 m 2 m 3 U m 4 m 1 m 3 m 2 ( s ) × ψ m 3 m 2 ; υ 3 υ 2 ( 2 ) ( s ; τ 3 ; τ 2 ) ψ m 1 ; ν 1 ( 1 ) * ( s ; τ 1 )
通过对薛定谔方程进行直接积分,可以计算单和双激子波函数。单激子波函数表示为
iħ ∂ ∂ t | ψ ν 1 ( 1 ) (t;τ1)>=H(t)| ψ ν 1 ( 1 ) (t;τ1)>
其中| ψ ν 1 ( 1 ) (t;t0)>= ∑ n ψ n ; ν 1 ( 1 ) ( t ; t 0 ) B n † | g > 。同理,类似的方程也可以应用于双激子波函数,
iħ ∂ ∂ t | ψ ν 1 ( 2 ) (t;τ2;τ1)>=H(t)| ψ ν 1 ( 2 ) (t;τ2;τ1)>
其中| ψ ν 1 ( 2 ) (t;τ2;τ1)>= 1 2 ∑ n 1 n 2 ψ n 1 n 2 ; υ 1 υ 2 ( 2 ) (t;τ2;τ1) B n 1 † B n 2 † g >。

3.4 SLE(stochastic Liouville equations)方法

用Liouville方程描述描述双模系统状态的密度矩阵的时间演化[32, 60]:
∂ ∂ t ρ(t)=- i ħ L(t)ρ(t)- i ħ Lint(t)ρ(t)
L(t)ρ(t)=- i ħ H 0 ( t ) , ρ ( t ) 代表孤立的系统演化,而Lint(t)ρ(t)=- i ħ H int ( t ) , ρ ( t ) 代表与辐射电场的耦合。
随机变量的概率分布P(Q,t)由Markovian主方程建模[32]:
∂ P ( Q , t ) ∂ t =-Γ(Q)P(Q,t)
其中Γ(Q)具有Smoluchowski过阻尼的布朗振子形式[32],
∂ P ( Q , t ) ∂ t = - ∑ j = 1 4 γ j ∂ ∂ Q j ( Q j + Δ j 2 ∂ ∂ Q j ) P ( Q , t )
随机Liouville方程通过将激子系统的Liouville方程和布朗振动子的四个马尔科夫主方程组合而成[32]。
ρ · (Q,t)=- i ħ L(Q)ρ(Q,t)-Γ(Q)ρ(Q,t)
SLE可以使用格林函数的矩阵连续分数表示在频域中求解。通过将频率ω2转换回时域来计算2DIR复相信号 S K I (ω3,t2,ω1) [32]。
S K I ( ω 3 , τ 2 , ω 1 ) = Im ∫ - ∞ ∞ d ω 2 S K I ( ω 3 , ω 2 , ω 1 ) e - i ω 2 τ 2
SLE可用于描述哈密顿量所有元素的多种类型的涨落。唯一的要求是,它们可以由几个满足马尔可夫运动方程的集合(离散或连续)坐标表示。这些方程通过描述联合系统+热库空间的演变来解释集体的热库坐标涨落对非线性红外光谱的影响。

4 2DIR技术及其在溶液化学中的应用

二维红外技术在与溶液动力学相关的众多领域,例如水氢键网络与能量输运、膜通道中的离子输运、蛋白质构象动力学、溶液反应过渡态以及多相催化反应动力学中都获得广泛地运用。
水溶液体系存在大量的可探测运动模式,以及非谐性和涨落性,开辟了许多分子间的输运途径,即使在平均耦合较小的情况下,也导致极化各向异性在观察到的时间尺度(80 fs)上完全衰减。发现共振能量转移对光子回波谱在极短的t2时间(<200 fs)中的影响很小。振动回波光谱技术(2DIR-PE)频谱中的大多数快速动力学是由局部O—H伸缩振动频率涨落引起的,这是由于局部非谐电势对氢键环境涨落的敏感性所致。O—H伸缩振动是水中氢键网络的绝佳探针。可以使用相同的方法模拟其他液体(如甲酰胺)的2DIR。在受限环境中进行水动力学研究具有重要的理论和实验意义[21, 61~63]。许多2DIR活动都集中在可逆胶束,特别是气溶胶(AOT)。对稀释的HOD在D2O或H2O液滴中的羟基伸缩吸收的研究表明[63],受限水的动力学比溶液中的慢。Fayer等使用受激振动回波和频谱解析的振动回波峰移动。表明受限水中氢键长度波动(50 fs)引起的最快动力学与溶液整体相似,但强束缚条件下与整体结构演化相关的较慢时间尺度(> 1 ps)会增加一个数量级[64,65]。可逆胶束中纯水的动力学也有大量研究[66]。红外泵浦探测和振动回波光谱技术支持两个独立的弛豫水子组件的存在。液滴核心的动力学类似于溶液,但水合壳层较慢。测得的外壳厚度为0.4 nm[67]。
钾通道负责钾离子在细胞间的跨膜选择性渗透。钾离子通过选择性过滤器渗透到单个细胞膜中,选择性过滤器是由4个钾离子结合位点的主链羰基排列构成的一个狭窄的孔。在2016年,Zanni等报告了选择性过滤器中对于特定位点(13C18O)同位素标记的半合成KcsA通道的二维红外光谱[24]。超快时间分辨率的二维红外光谱可提供此过滤器中自发发生的多离子配置和结构分布的瞬时构型。通过解析两个特征性的延伸部位,Martin Zanni揭示了两个结构构象的统计权重。二维红外光谱通过分子动力学模拟重现其结构,其中水在结合位点分离了两个K +,排除了占据相邻位点的离子构型。
瞬态2D红外光谱结合了皮秒时间分辨率和感应溶液相中特定分子基团之间的局部接触的能力。分子动力学模拟具有相似的长度和时间尺度,可用于研究超快非平衡动力学过程,从而使这两种方法获得的结果之间的比较变得直接而直接,对于它们的相互验证和解释很有用。因此,可以预计瞬态2D-IR光谱技术和分子动力学模拟的结合使用将为快速生物分子过程提供空前的洞察力。二维红外光谱法则可用来绘制分子组之间的振动耦合,并因此映射它们的相对位置和方向,现在通常用于研究皮秒级时标上的平衡过程。该方法扩展到非平衡状态使得实验上可以在短肽中实时观察到分子内氢键的减弱和beta转接的同时打开。2005年,Hamm等发现此过程的速度比为蛋白质侧链之间的接触形成而建立的“折叠速度极限”快两个数量级[24]。我们对超快动力学的二维红外(2DIR)研究使用了环状二硫键桥接的肽环(Boc-Cys-Pro-Aib-Cys-OMe)。根据核磁共振结果,其二硫键和分子内氢键使肽非常坚硬,并确保采用唯一的beta发卡结构。Tokmakoff等[68,69,70,71,72,73]和庄巍等[32, 74]都曾通过理论模拟对于Trpzip肽链的beta发卡的解离动力学进行一系列细致的研究。
化学反应的许多性质取决于连接反应物和产物的过渡态,但是很难直接获得有关液体中这些短寿命结构的任何信息。研究表明,二维红外光谱学可以通过跟踪分子越过过渡态时振动模式的转变来提供有关过渡态的直接信息。2008年,Harris等[75]成功地通过二维红外光谱探测了一个简单的化学反应,Fe(CO)5的重排反应,其中轴向和赤道的二氧化碳配体的交换引起分子简正模式之间的振动能交换。二维红外光谱学为这种能量转移提供了有关时间尺度、过渡状态和反应机理的直接证据。
科学家们使用二维红外光谱技术探测到作为光还原催化剂的二氧化硅表面束缚的过渡金属羰基配合物氯化三羰基1,10-菲咯啉,fac-RePhen(CO)3Cl的界面动力学和结构[76]。通过理论框架解释实验数据,探讨在分离结构演化和激发转移在诱导光谱扩散中的作用。正如表面结合的复合物的羰基拉伸振动所显现出的那样,其结构动力学在无溶剂的情况下具有约150皮秒的特征时间,而在添加氯仿溶剂时持续时间减少了三倍,比体相溶液的降低了一个的数量级。相反,当将溶剂应用于单层时,溶剂与络合物的相互作用可使探测振动的寿命延长160%

5 和频振动光谱技术及其在表面和界面化学中的应用

和频振动光谱技术在凝聚态相关的表面和界面研究中具有不可替代的作用。和频振动光谱能够选择性地测量表面或者界面分子的振动及电子光谱信号,比如在测量空气和书界面的水分子光谱和结构中,测量到的和频光谱信号只是来源于界面上的一两层水分子的贡献,而体相中大量的水分子并不贡献和频信号,除非界面上有高密度的电荷密度产生的表面电位[17,18,36,77]。更为重要的是,和频过程中的三束光(两束入射激光和一束出射信号光)正好构成一个三维的坐标系,因而和频过程对于界面上溶液中的任何具有手性(Chirality)的分子结构或其他类型的立体结构具有选择性测量的能力。这为研究自然界和生命科学中普遍存在的微观(microscopic)和介观(mesoscopic)的手性结构和手性相互作用及立体化学反应等现象提供了有力的研究工具[35, 78,79]。
物质世界和生命世界中普遍存在着非均相的结构。非均相结构的基本特征是表面和界面的存在。在图1a中的所有不同状态的物质之间,都会普遍存在着表面和界面,而任何一个表面或者界面都至少是一个凝聚态的边界(气/液和气/固界面,也分别称为液体和固体表面)或者两个凝聚态之间的边界(液/固,液/液和固/固界面)。在表面和界面上,原子和分子因为受到了两相之间不对称的相互作用而被极化和发生结构与构象的变化,产生取向和自组装与聚集。因为排列与自组装,在表面和界面上分子之间的相互作用,以及它们与两相中接近于界面的分子之间的相互作用有着非常显著的立体效应。比如在生物矿化和复合材料晶体生长的过程,是由非常复杂和精细的无机/有机/生物大分子在界面上的相互作用来调控的。这些方面的研究也是目前凝聚态化学领域与表面和界面作用密切相关的研究前沿,和频振动光谱也进入了这些相关领域的研究[80,81,82]。催化与生命过程中重要的化学反应,与表面和界面的上的特定的立体效应(steric effect)也存在着重要的关系。因而仅从研究气相或者相对均匀的凝聚态这样的相对均匀环境中的原子、分子或者离子的结构、相互作用以及动态过程进行研究所获得的知识往往不能够被简单地推广到表面和界面的分子上。比如,在均匀的液体中长程相互作用一般可以用连续介质理论进行处理,但在界面上的长程作用则由于界面的不连续性和不对称性不能照搬,其理论处理更为复杂[15, 83]。因此,鉴于表面和界面结构、构象和相互作用动力学在异相过程,如工业催化与生物膜上的蛋白-药物相互作用等直接与人类能源与健康相关的领域中的重要性,原位测量表面和界面上的分子的结构、构象和动力学过程成为非常重要的基本科学问题。同样重要的也包括通过比较界面与气相或者溶液中的分子结构、构象和动力学过程之间的差别,从而了解这些差别的原因和对不同化学环境下的化学过程的影响,推进表面与界面化学结构与动力学理论和计算方法的发展。
图8中总结了和频振动光谱在广泛的表面和界面化学问题中的应用。图9则给出了不同类型的和频振动光谱技术在研究表面和界面的原子或分子的振动态和电子态,以及振动态和电子态耦合现象中的作用。由于和频光谱中的两束入射光可以分别对应于与分子振动态和电子态的共振相互作用,因此,和频光谱可以有路线不同的形式,分别对应于测量分子的不同性质:(a)单共振和频振动光谱,基态振动态共振;(b)红外+可见双共振和频振动光谱,基态振动态和电子激发态双共振;(c)可见+红外双共振和频振动光谱,电子激发态和激发态振动态双共振;(d)可见+可见双共振和频电子光谱。其中b,c,d三种情形可以用于研究电子激发态相关的表面界面分子结构、传能及电子与质子转移过程等。
图8 和频振动光谱在化学、材料、能源、环境和生命科学领域中的广泛应用和解决的科学问题[36]

Fig.8 Broad applications of sum frequency generation vibrational spectroscopy to various scientific problems in the fields of chemistry, materials, energy, environment, and life sciences[36]

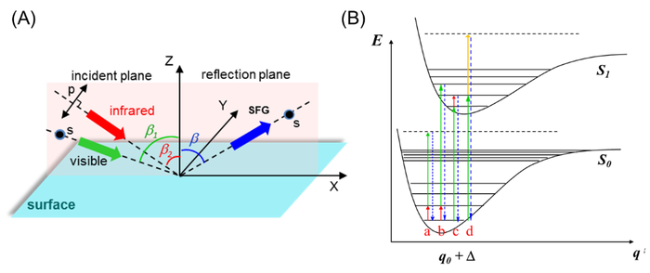
图9 和频振动光谱原理示意。(A)共传播构型下的和频振动光谱的ssp偏振组合中和频振动光谱信号、入射的可见和红外光处于与界面垂直的共同入射平面中,其中光场的偏振方向p是指光电场方向在入射平面内,而偏振方向s是指光电长矢量方向与入射面垂直;(B)和频振动光谱的不同形式。(a)单共振和频振动光谱,基态振动态共振;(b)红外+可见双共振和频振动光谱,基态振动态和电子激发态双共振; (c)可见+红外双共振和频振动光谱,电子激发态和激发态振动态双共振;(d)可见+可见双共振和频电子光谱。(b、c、d)三种情形可以用于研究电子激发态相关的表面界面分子结构、传能及电子与质子转移过程等[36]

Fig.9 Illustration of the SFG-VS.(A) Showing the infrared(IR) and visible(Vis) beams incident in the same plane in a co-propagating geometry, with the SFG signal, the visible beam and the IR beam in the ssp polarization combination. The polarization of the optical field is defined as p polarization when the optical filed vector is within the incident plane, and it is s polarization when the optical field is perpendicular to the incident plane.(B) Various types of SFG processes that can be used to study ground state vibrational spectra and electronic spectra of molecular surfaces and interfaces. Type (a) is called the IR-SFG-VS, the most common single resonance SFG-VS with only the IR frequency in resonance with the ground state vibrational transition of the molecule of interest; Type (b) is called the IR-Vis double resonance SFG-VS(IR-Vis SFG-VS), where the IR frequency is in resonance with the ground state and the visible is in resonance with the electronic resonance of the molecule; Type (c) is called the Vis-IR double resonance SFG-VS(Vis-IR DR-SFG-VS); and the Type (d) is the Vis-Vis SFG-VS[36]

目前绝大多数的和频振动光谱测量都是单共振的和频光谱研究(a),只有较少的双共振和频光谱研究。双共振和频振动光谱最早由沈元壤等实现[84],随后王鸿飞等发现了b/c两种不同双共振和频振动过程的干涉效应[85]。从双共振和频光谱能够同时与分子的振动态和电子态相互作用原理来分析,不同形式的双共振和频振动光谱技术将是测量异相化学反应中的分子结构、传能及电子与质子转移过程的重要工具。与双共振和频光谱有关的理论框架和方法已经在密度矩阵描述的分子动力学的基础上发展起来,这些都为双共振和频光谱在凝聚态表面和界面的进一步研究奠定了良好的基础[86]。

6 结论及展望

本文简要地总结和介绍了二维红外光谱及和频振动光谱在研究凝聚态中化学物质和化学反应的复杂结构、热力学特性和动力学过程中的基本的原理、方法和应用。
物质的凝聚态和凝聚态的表界面广泛存在,然而对凝聚态和表界面的化学过程的细致认识和准确研究还有很多的工作需要开展。凝聚态及其表面与界面化学的基础理论和实验方法的研究是一个广泛的领域和现代物理化学和化学物理研究的前沿。由于凝聚态物质及其表界面的结构复杂性和动态特性,描述这些过程需要用到复杂的量子力学、统计力学和最先进的计算技术和计算工具,测量这些过程也依赖于前沿的超快激光和灵敏的检测技术的不断发展。这些研究的目的是为了理解控制和影响凝聚态及其表面与界面的化学过程的结构、热力学和动力学过程的机制和机理,从而能够为控制和操纵凝聚态中的化学变化和化学反应提供基本概念、理论基础和实验及检测表征手段。
基于非线性光谱学的各种动力学振动光谱技术是不断发展的研究凝聚态及其表面与界面相互作用和化学反应的有效工具。其中二维红外光谱(2D-IR)则是光与物质作用的三界非线性光学效应,而和频振动光谱(SFG-VS)是光与物质作用的二阶非线性光学效应。二阶非线性光学效应具有独特的表面和界面选择性,因此相关的和频光谱技术可以用来研究凝聚态的表面与界面化学。三阶的非线性光学技术则可以用于研究凝聚态,尤其是液体和无序物质(disordered matter)的光谱、结构与动力学。
在三阶非线性光谱方面,近来还发展出了测量溶液和凝聚态体相中的振动态和电子态耦合动力学二维振动态电子态光谱(2D-VE,即2D-vibrational/electronic spectroscopy)和二维电子态振动态光谱(2D-EV,2D-electronic/vibrational spectroscopy)[87,88,89]。这些方兴未艾的新技术和新方法,与上面提到的双共振和频振动光谱方法用于表界面和手性结构中的振动态和电子态耦合的方法正好能够互补,有望继续发展成为研究凝聚态及其表面和界面的振动态和电子态耦合的技术和方法,进一步推进凝聚态及其表界面的化学基础理论和实验检测技术的发展。

References

Publishing order | Descend order by publishing year | Descend order by cited within
[1]
Polanyi J C, Zewail A H. Acc. Chem. Res., 1995,28(3):119.

DOI

[2]
Avouris P. Acc. Chem. Res., 1995,28(3):95.

DOI

[3]
Xu R. Natl. Sci. Rev., 2018,5:1.

DOI

[4]
Xu R, Wang K, Chen G, Yan W. Natl. Sci. Rev., 2018,6(2):191.

DOI

[5]
Levine R D. Molecular Reaction Dynamics. Oxford: Cambridge University Press, 2009.

[6]
Nitzan A, Press O U. Chemical Dynamics in Condensed Phases: Relaxation, Transfer and Reactions in Condensed Molecular Systems. Oxford: Oxford University Press, 2006.

[7]
Eisenthal K B. Chem. Rev., 1996,96:1343.

DOI PMID

[8]
Arnolds H, Bonn M. Surf. Sci. Rep., 2010,65(2):45.

DOI

[9]
Robinson G W, Singh S, Krishnan R, Zhu S B, Lee J. J. Phys. Chem., 1990,94(1):4.

DOI

[10]
Shelby R M, Harris C B, Cornelius P A. J. Chem. Phys., 1979,70(1):34.

DOI

[11]
Oxtoby D W. Annu. Rev. Phys. Chem., 1981,32:77.

DOI

[12]
Hynes J T. Annu. Rev. Phys. Chem., 1985,36:573.

DOI

[13]
Hynes J T. Annu. Rev. Phys. Chem., 2015,66:1.

DOI PMID

[14]
Owrutsky J C, Raftery D, Hochstrasser R M. Annu. Rev. Phys. Chem., 1994,45:519.

PMID

[15]
Benjamin I. Chem. Rev., 1996,96(4):1449.

DOI PMID

[16]
Ball P. Chem. Rev., 2008,108(1):74.

DOI PMID

[17]
Gan W, Wu D, Zhang Z, Feng R R, Wang H F. J. Chem. Phys., 2006,124:114705.

DOI PMID

[18]
Feng R R, Guo Y, Wang H F. J. Chem. Phys., 2014, 141: 18C507.

DOI PMID

[19]
Nihonyanagi S, Mondal J A, Yamaguchi S, Tahara T. Annu. Rev. Phys. Chem., 2013,64:579.

DOI PMID

[20]
Bagchi B. Chem. Rev., 2005,105:3197.

DOI PMID

[21]
Pal S K, Zewail A H. Chem. Rev., 2004,104:2099.

DOI PMID

[22]
Frauenfelder H, Chen G, Berendzen J, Fenimore P W, Jansson H, McMahon B H, Stroe I R, Swenson J, Young R D. Proc. Natl. Acad. Sci. U. S. A., 2009,106:5129.

DOI PMID

[23]
Hamm P, Zanni M. Concepts and Methods of 2D Infrared Spectroscopy. Oxford: Cambridge University Press, 2011.

[24]
Kratochvil H T, Carr J K, Matulef K, Annen A W, Li H, Maj M, Ostmeyer J, Serrano A L, Raghuraman H, Moran S D, Skinner J L, Perozo E, Roux B, Valiyaveetil F I, Zanni M T. Science, 2016,353:1040.

DOI PMID

[25]
Cho M. Two-Dimensional Optical Spectroscopy. CRC Press, 2009.

[26]
Cho M. Coherent Multidimensional Spectroscopy. Singapore: Springer, 2019.

[27]
Cho M H. Chem. Rev., 2008,108:1331.

DOI PMID

[28]
Fayer M D. Ultrafast Infrared Vibrational Spectroscopy. Taylor & Francis, 2013.

[29]
Qin Y Z, Wang L J, Zhong D P. Proc. Natl. Acad. Sci. U. S. A., 2016,113:8424.

DOI PMID

[30]
Lind P A, Daniel R M, Monk C, Dunn R V. (BBA)-Proteins Proteom, 2004,1702(1):103.

[31]
Rinne K F, Gekle S, Netz R R. J. Phys. Chem. A, 2014,118(50):11667.

DOI PMID

[32]
Mukamel S. Principles of Nonlinear Optical Spectroscopy. Oxford University Press, 1995.

[33]
Shen Y R. Fundamentals of Sum-Frequency Spectroscopy. Cambridge: Cambridge University Press, 2016.

[34]
Morita A. Theory of Sum Frequency Generation Spectroscopy. Singapore: Springer, 2018.

[35]
Wang H F, Velarde L, Gan W, Fu L. Annu. Rev. Phys. Chem., 2015,66:189.

DOI PMID

[36]
Wang H F. Prog. Surf. Sci., 2016,91(4):155.

DOI

[37]
Zhuang W, Hayashi T, Mukamel S. Angew. Chem. Int., 2009,48(21):3750.

DOI

[38]
Wang H F, Gan W, Lü R, Rao Y, Wu B H. Int. Rev. Phys. Chem., 2005,24(2):191.

DOI

[39]
Buck M, Himmelhaus M. J. Vac. Sci. Technol. A. 2001,19(6):2717.

DOI

[40]
Tian C S, Shen Y R. Surf. Sci. Reps., 2014,69(2/3):105.

[41]
Richter L J, Petralli-Mallow T P, Stephenson J C. Opt. Lett. 1998,23(20):1594.

DOI PMID

[42]
Shen Y R. Annu. Rev. Phys. Chem., 2013,64:129.

DOI PMID

[43]
Smith J P H S V. Anal. Chem., 2004, 76(15): 287 A.

[44]
Hu X H, Wei F, Wang H, Wang H F. J. Phys. Chem. C, 2019,123(24):15071.

DOI

[45]
Laaser J E, Xiong W, Zanni M T. J. Phys. Chem. B, 2011,115(11):2536.

DOI PMID

[46]
Laaser J E, Zanni M T. J. Phys. Chem. A, 2013,117(29):5875.

DOI PMID

[47]
Zhang Z, Piatkowski L, Bakker H J, Bonn M. Nat. Chem., 2011,3:888.

DOI PMID

[48]
Wang J, Clark M L, Li Y, Kaslan C L, Kubiak C P, Xiong W. J. Phys. Chem. Lett., 2015,6(21):4204.

DOI PMID

[49]
Mukamel S. Annu. Rev. Phys. Chem., 2000,51:691.

PMID

[50]
Velarde L, Wang H F. Phys. Chem. Chem. Phys., 2013,15:19970.

DOI PMID

[51]
Xu J, Xu R X, Abramavicius D, Zhang H D, Yan Y J. Chin. J. Chem. Phys., 2011,24(5):497.

DOI

[52]
Mukamel S, Abramavicius D. Chem. Rev., 2004,104(4):2073.

DOI PMID

[53]
Simpson N, Hunt N T. Int. Rev. Phys. Chem., 2015,34(3):361.

DOI

[54]
Kubo R. J. Math. Phys., 1963,4(2):174.

DOI

[55]
Jansen T L, Zhuang W, Mukamel S. J. Chem. Phys., 2004,121:10577.

DOI PMID

[56]
Jansen T L, Knoester J. J. Chem. Phys., 2006,124:044502.

DOI PMID

[57]
Jansen T L, Knoester J. J. Phys. Chem. B, 2006,110(45):22910.

DOI PMID

[58]
Auer B M, Skinner J L. J. Chem. Phys., 2007,127(10):104105.

DOI PMID

[59]
Jansen T L C, Ruszel W M. J. Chem. Phys., 2008,128(21):214501.

DOI PMID

[60]
Tanimura Y, Kubo R. J. Phys. Soc. Jpn., 1989,58:101.

DOI

[61]
Woutersen S, Mu Y G, Stock G, Hamm P. Proc. Natl. Acad. Sci. U. S. A., 2001,98(20):11254.

DOI PMID

[62]
Idrissi A, Bartolini P, Ricci M, Righini R. Phys. Chem. Chem. Phys., 2003,5:4666.

DOI

[63]
Cowan M L, Bruner B D, Huse N, Dwyer J R, Chugh B, Nibbering E T J, Elsaesser T, Miller R J D. Nature, 2005,434:199.

DOI PMID

[64]
Piletic I R, Tan H S, Fayer M D. J. Phys. Chem. B, 2005,109:21273.

DOI PMID

[65]
Tan H S, Piletic I R, Riter R E, Levinger N E, Fayer M D. Phys. Rev. Lett., 2005,94:057405.

DOI PMID

[66]
Fenn E E, Wong D B, Giammanco C H, Fayer M D. J. Phys. Chem. B, 2011,115(40):11658.

DOI PMID

[67]
Moilanen D E, Wong D, Rosenfeld D E, Fenn E E, Fayer M D. Proc. Natl. Acad. Sci. U S A., 2009,106(2):375.

DOI PMID

[68]
Cheatum C M, Tokmakoff A, Knoester J. J. Chem. Phys., 2004,120:8201.

DOI PMID

[69]
Smith A W, Tokmakoff A. J. Chem. Phys., 2007,126:045109.

DOI PMID

[70]
Smith A W, Tokmakoff A. Angew. Chem. Int. Ed., 2007,46(42):7984.

DOI

[71]
Smith A W, Lessing J, Ganim Z, Peng C S, Tokmakoff A, Roy S, Jansen T L C, Knoester J. J Phys. Chem. B, 2010,114(34):10913.

DOI PMID

[72]
Roy S, Lessing J, Meisl G, Ganim Z, Tokmakoff A, Knoester J, Jansen T L C. J. Chem. Phys., 2011,135:234507.

DOI PMID

[73]
Lessing J, Roy S, Reppert M, Baer M, Marx D, Jansen T L, Knoester J, Tokmakoff A. J. Am. Chem. Soc., 2012,134(11):5032.

DOI PMID

[74]
Zhuang W, Sgourakis N G, Li Z Y, Garcia A E, Mukamel S. Proc. Natl. Acad. Sci. U S A., 2010,107(36):15687.

DOI PMID

[75]
Cahoon J F, Sawyer K R, Schlegel J P, Harris C B. Science, 2008,319(5871):1820.

DOI PMID

[76]
Rosenfeld D E, Gengeliczki Z, Smith B J, Stack T D P, Fayer M D. Science, 2011,334(6056):634.

DOI PMID

[77]
Ohno P E, Wang H F, Geiger F M. Nat. Comm., 2017,8:1032.

DOI

[78]
Yan E C Y, Fu L, Wang Z, Liu W. Chem. Rev., 2014,114(17):8471.

DOI PMID

[79]
Hu X H, Fu L, Hou J, Zhang Y N, Zhang Z, Wang H F. J. Phys. Chem. Lett., 2020,11(4):1282.

DOI PMID

[80]
Shao C Y, Jin B, Mu Z, Lu H, Zhao Y Q, Wu Z F, Yan L M, Zhang Z S, Zhou Y C, Pan H H, Liu Z M, Tang R K. Sci. Adv., 2019, 5(8): eaaw9569.

DOI PMID

[81]
De Yoreo J J, Gilbert P U P A, Sommerdijk N A J M, Penn R L, Whitelam S, Joester D, Zhang H Z, Rimer J D, Navrotsky A, Banfield J F, Wallace A F, Michel F M, Meldrum F C, Cölfen H, Dove P M. Science, 2015, 349(6247): aaa6760.

DOI PMID

[82]
Tuladhar A, Chase Z A, Baer M D, Legg B A, Tao J H, Zhang S, Winkelman A D, Wang Z M, Mundy C J, De Yoreo J J, Wang H F. J. Am. Chem. Soc., 2019,141(5):2135.

DOI PMID

[83]
Wang H, Borguet E, Eisenthal K B. J. Phys. Chem. B, 1998,102(25):4927.

DOI

[84]
Raschke M B, Hayashi M, Lin S H, Shen Y R. Chem. Phys. Lett., 2002,359(5/6):367.

DOI

[85]
Wu D, Deng G H, Guo Y, Wang H F. J. Phys. Chem. A, 2009,113(21):6058.

DOI PMID

[86]
Yang L, Niu Y L, Lin C K, Hayashi M, Zhu C Y, Lin S H. In: Advances in Chemical Physics, 2014. 295.

[87]
Dong H, Lewis N H C, Oliver T A A, Fleming G R. J. Chem. Phys., 2015,142(17):174201.

DOI PMID

[88]
Oliver T A A, Lewis N H C, Fleming G R. Proc. Natl. Acad. Sci. U. S. A., 2014,111(28):10061.

DOI PMID

[89]
Courtney T L, Fox Z W, Slenkamp K M, Khalil M. J. Chem. Phys., 2015,143(15):154201.

DOI PMID

Options
Outlines

/

〈 〉