English
往期目录
新闻公告
More

化学进展 >

2022 , Vol. 34 >Issue 12: 2619 - 2637

DOI: https://doi.org/10.7536/PC220524

综述

机器学习辅助高通量筛选金属有机骨架材料

  • 李炜 , 1, * ,
  • 梁添贵 1 ,
  • 林元创 1 ,
  • 吴伟雄 1 ,
  • 李松 2
展开
  • 1 暨南大学能源电力研究中心 珠海 519070
  • 2 华中科技大学能源与动力工程学院 武汉 430074

李炜 博士,副教授。2015年与2020年于华中科技大学获得学士和博士学位. 2021年加入暨南大学能源电力研究中心从事金属有机骨架材料高通量筛选及其在能源存储与转化方面的应用研究。

收稿日期: 2022-05-16

  修回日期: 2022-07-08

  网络出版日期: 2022-09-19

基金资助

中央高校基本科研业务经费(21621039)

广州市基础与应用基础研究基金项目(202201010433)

中国博士后面上项目(2021M701413)

收起

Machine Learning Accelerated High-Throughput Computational Screening of Metal-Organic Frameworks

  • Wei Li , 1 ,
  • Tiangui Liang 1 ,
  • Yuanchuang Lin 1 ,
  • Weixiong Wu 1 ,
  • Song Li 2
Expand
  • 1 Energy and Electricity Research Center, Jinan University,Zhuhai 519070, China
  • 2 School of Energy and Power Engineering, Huazhong University of Science and Technology,Wuhan 430074, China
* Corresponding author e-mail:

Received date: 2022-05-16

  Revised date: 2022-07-08

  Online published: 2022-09-19

Supported by

Fundamental Research Funds for the Central Universities(21621039)

GuangZhou Basic and Applied Basic Research Foundation(202201010433)

China Postdoctoral Science Foundation(2021M701413)

Fold

摘要

金属有机骨架(Metal-organic Frameworks, MOFs)材料具有高比表面积、大孔容和可调控合成等优点,在气体储存、吸附分离、催化等领域受到了广泛关注,近年来其数量呈爆炸式增长的趋势。而高通量计算筛选(High-throughput Computational Screening, HTCS)是从大量材料中发现高性能目标材料与挖掘构效关系最有效的研究方法。在高通量计算筛选过程中产生的数据具有量大、维度多等特点,尤其适合采用机器学习(Machine Learning, ML)进行训练,从而进一步提升筛选效率、深入挖掘多维数据间的构效关系。本综述概述了机器学习辅助高通量筛选金属有机骨架材料的一般流程与常用方法,包括常用描述符、算法与评价标准等,对其在气体储存、分离及催化等领域的研究进展进行了总结,以此明确当前研究中面临的挑战与后续发展方向,助力MOFs材料设计研发。

关键词： 金属有机骨架; 机器学习; 高通量筛选; 分子模拟; 吸附

本文引用格式

李炜 , 梁添贵 , 林元创 , 吴伟雄 , 李松 . 机器学习辅助高通量筛选金属有机骨架材料[J]. 化学进展, 2022 , 34(12) : 2619 -2637 . DOI: 10.7536/PC220524

Abstract

Metal-organic frameworks (MOFs) with ultrahigh surface area, large pore volume and tunable pore environment are regarded as promising adsorbents in gas adsorption and separation. With the exploding number of possible MOFs, it is an imperative challenge to discover high-performing MOFs for a specific application. High-throughput computational screening (HTCS) has been frequently adopted to identify the suitable adsorbents with remarkably reduced computational time and cost in the past decades. Recently, machine learning (ML) is used to accelerate the HTCS process and explore the structure-property relationship. In this review, we summarize the ML algorithms for gas storage, separation and catalysis by MOFs. Four categories of descriptors widely used in ML are reviewed, including geometrical descriptor (i.e., pore size, surface area), topological descriptor (i.e., pore connectivity, cavity size), chemical descriptor (i.e., atom type, degree of unsaturation), and energy-based descriptor (i.e., cohesive energies, Voronoi energies). Unsupervised learning and supervised learning, such as linear regression (LR), artificial neural network (ANN), support vector machine (SVM), and random forest (RF) are introduced and a complete overview of how these ML algorithms are effectively utilized to assist MOF discovery is provided. Recent research progress on ML algorithms in various applications, such as H2, CH4 storage, carbon capture, noble gas, Cx/Cy separation and catalysis are presented in this work. It is anticipated that ML will play a more vital role in identifying top candidates with increasing number of MOFs. Thus, this review aims to outline fundamental knowledge of ML algorithms for MOF discovery in the fields of gas storage, separation and catalysis.

Contents

1 Introduction

2 Methodology

2.1 High-throughput computational screening

2.2 Machine learning

3 Machine learning accelerated MOFs screening

3.1 Gas storage

3.2 Gas separation

3.3 MOFs physicochemical property

4 Conclusion and outlook

Key words： metal-organic frameworks; machine learning; high-throughput computational screening; molecular simulation; adsorption

1 引言

多孔材料由相互贯通或封闭的孔洞构成网络状结构,传统的多孔材料包括活性炭[1]、沸石[2]、分子筛[3]等,是常见的吸附剂类别。近年来,金属有机骨架(Metal-organic Frameworks,MOFs)、共价有机骨架(Covalent Organic Frameworks,COFs)与碳纳米管等新型多孔材料受到了广泛关注。其中,MOFs是由无机金属单元(金属离子、团簇或链)与有机配体(羧酸盐、磷酸酯、或含氮配体等)连接而成的周期性晶体结构[4],具有良好的热稳定性(~ 500 ℃)、高比表面积(> 8000 m2/g)、低密度(~ 0.2 g/cm3)及丰富的纳米孔道(3 Å ~ 100 Å)等优势[5]。研究人员通过对不同结构单元、连接方式和拓扑结构的组合,调控物理和化学性质,制备拥有优异性能的MOFs材料,应用于气体吸附与分离[6⇓⇓~9]、热泵[10,11]、催化[12⇓~14]、电池[15]等领域。
MOFs的发展十分迅速,如图1A所示,实验合成的结构(experimental MOFs,eMOFs)迄今已逾九万种,大部分收录于剑桥晶体结构数据库(Cambridge Structural Database,CSD)中[16]。随着高性能计算与模拟技术的发展,研究人员也依据化学规律生成MOFs材料,如2011年Wilmer等[17]基于“自顶向下”方法设计构建了137 953种假设的MOFs(hypothetical MOFs,hMOFs)数据库;在2017年Colón等[18]利用了基于边缘传递拓扑网络(Edge-Transitive Topological Nets)算法与ToBaCCo代码构建了含41种拓扑结构,共13 512种hMOFs组成的数据库。但仍有近乎无限种类的MOFs可设计合成,如此庞大的数量一方面使我们可以从中发现适用于各类应用下的MOFs;另一方面,仅依靠实验搜寻与制备高性能MOFs,需要漫长的周期与高昂的研发成本,仿佛大海捞针。
图1 (A)1972年至2022年CSD数据库中MOFs数目增长趋势; (B)高通量筛选流程示意图

Fig. 1 Schematic diagram of (A)growth trends of the number of MOFs in CSD database from 1972 to 2022.(B)high-throughput computational screening methodology

基于分子模拟的高通量计算筛选(High-Throughput Computational Screening,HTCS)技术是评估与优选MOFs最高效的研究方法。其一般流程如图1B所示:1)构建或选定MOFs筛选数据库;2)采用比表面积或孔径等特征进行预筛选;3)分子模拟预测MOFs的吸附分离、催化等各项性能;4)结合实际应用条件,计算衡量指标进行综合评价, 获得高性能MOFs[4]。
但随着MOFs种类爆炸式的增长,全面评估其在各类场景下的应用性能,纵使高通量筛选技术也力有不逮,且高通量筛选产生的海量、多维度数据也需要借助大数据技术深入分析。机器学习(Machine Learning,ML)与此需求相契合,用其辅助高通量筛选是近年来的研究热点。机器学习基于高维数据中隐藏的统计学规律,通过训练高通量筛选数据集,预测MOFs吸附剂的吸附量[19,20]、选择性[21,22]、等温吸附曲线[23]等材料特性,辅助加速发现高性能吸附剂,常用的机器学习算法包括人工神经网络[24](Artificial Neural Networks,ANN)、梯度提升机[25](Gradient Boosting Machine,GBM)等。
本文概述机器学习辅助高通量筛选研发新型吸附剂的研究进展。因为此类研究中算法大部分基于TensorFlow[26]、Pytorch[27]、Scikit-learn[28]等开源软件,本文重点关注的是这些算法发掘的构效关系,或其训练模型的预测性能及泛化能力。并以此讨论大数据技术在MOFs研发领域的发展趋势及其面临的挑战。

2 方法

在高通量筛选的基础上,机器学习辅助研究的一般流程如上图2所示。高通量筛选部分包括a. 数据库选取、预筛选,与b. 分子模拟等过程,相结合的机器学习部分则包括c. 描述符选取、参数优化与d. 模型训练、性能预测及e. 数据分析等,后续可开展f. 实验验证目标MOFs性能或更进一步提出新型高性能结构合成、设计策略。
图2 机器学习辅助高通量筛选的常用流程

Fig. 2 The general procedure of ML-assisted high-throughput computational screening of MOFs for application

2.1 高通量筛选技术

选取合适的数据库是高通量筛选研究的基础,也会影响机器学习算法的性能。MOFs数据库主要分为eMOFs与hMOFs两类[4]。其中eMOFs是从实验中收集到的晶体结构文件整理而成,如Snurr等[29]建立的CoRE MOFs (Computation-Ready Experimental MOFs)数据库,皆有完备的合成方法,其特点在于结构多样性显著;而hMOFs数据库则是依据化学规律生成而来,如李松等[30]构建的MTV MOF(Multivariate MOF)数据库,材料结构清晰,具有明显的规律性。
对数据库进行预筛选时,一般采用Zeo++[31]、RASPA[32]、LAMMPS[33]等计算或收集数据库中MOFs几何性质、拓扑结构、化学信息及吸附势分布等参数,并根据应用场景选择合适范围来排除不符合条件的MOFs样本,降低计算量。常用的包括最大孔直径(Largest Cavity Diameter,LCD)、受限孔直径 (Pore Limited Diameter,PLD)、密度(Density,ρ)、孔隙率(Void Fraction,VF)、孔容(Available Pore Volume,Va)、比表面积(Accessible Surface Area,ASA)、重量比表面积(Gravimetric Surface Area,GSA)等。
分子模拟技术是高通量筛选中预测MOFs性能的主要方法,一般是巨正则蒙特卡洛模拟[5,34] (Grand Canonical Monte Carlo,GCMC)平衡态吸附性能等性质,分子动力学模拟[35](Molecular Dynamics,MD)动态扩散等性质。此外,也有部分研究基于经典密度泛函的cDFT[36](classical DFT)和lattice GCMC[37]预测MOFs性质,开展高通量筛选研究。

2.1.1 MOFs的蒙特卡洛模拟

GCMC模拟可用于模拟MOFs的吸附行为。模拟中指定的是吸附质的化学势,体系中的体积(V)、温度(T)、化学势(μ)保持恒定,不考虑气体分子在MOFs中的动力学性质,通过对气体分子在MOFs中的插入、删除、移动和旋转等微观态来获得体系的平衡分布[38]。通过蒙特卡洛模拟,可以获得材料的热力学性质。由状态方程或独立的体相模拟,易得MOFs的吸附量与分压比的联系,从而获得材料中气体的等温吸附曲线[39]。在具有固定温度、体积和分子数的正则系综中,亨利常数、结合能等数据也可以通过GCMC模拟计算而得[40] 。

2.1.2 分子动力学模拟

MD模拟在恒定体积、温度或压力的工况中进行[40]。根据牛顿力学原理,MD模拟建立所有气体分子的运动方程,通过相互作用势解出动力学参数, 而后得到气体分子在MOFs中的运动轨迹随时间的变化产生的一系列微观态[38]。并进一步根据MD模拟的分子轨迹确定扩散系数[41]、电导率[42]等动力学性质。

2.2 机器学习方法

基于分子模拟的高通量筛选方法虽然可以评估成千上万吸附剂的性能,然而随着MOFs数量的爆炸式增长与应用场景的不断拓展,仍力有不逮。而机器学习(ML)可辅助高通量筛选技术,优选描述符,构建数据集训练机器学习模型,高效预测MOFs各类性能,并解析构效关系。
构建ML模型的前置步骤是描述符的选取与转换,转换时应保持目标属性不变[43,44]。常用的描述符如下图3所示,包括几何参数、拓扑结构、化学性质与能势信息。几何参数是普遍采用的描述符,一般在预筛选中便可获得,包括孔容、孔径、密度与孔隙率等[4]。拓扑结构则包括孔道连接性、孔隙形态与孔道分布等描述符。
图3 描述符的分类

Fig. 3 The classification of descriptors

如Krishnapriyan等[45]开发持久性图像法(Persistence Image Approach),将拓扑描述符与正则化的结构特征结合,矢量化后作为机器学习模型的输入,以此成功预测了沸石的吸附性能。以上描述符较为贴近实验测量数据,可直观反应MOFs基本性质,但基于此训练的机器学习模型泛化性较差。而在化学性质方面,诸如原子类型、不饱和金属位点、金属团簇比例、原子电负性与亨利系数(Henry’s constant,KH)也是常用的描述符,此类数据分布区间较广,通常应对其进行特征转化,如常对KH对数归一化。更进一步,学者们也深入分析分子内聚能[46](Cohesive Energy)、Voronoi能[47]及能量分布函数[48]等分子内部势能微观信息,以此提升模型预测精度以及泛化性。如Rosen等[46]利用密度泛函理论(Density Functional Theory,DFT)构建了一个拥有材料量子化学性质的QMOFs数据库,其中包含了15 713种eMOFs的原子类型、能量、几何参数、电荷密度、旋转密度等能量信息,以此训练ML算法准确预测MOFs的能带带隙。
为避免过拟合,机器学习训练时会采用k-Flod等交叉验证[49](Cross Validation)方法,将数据集分为训练数据集、验证数据集与测试集,根据训练的结果选用合适的比例分割。一般而言,训练集与测试集的比例在20% ~ 80%间变动。
ML模型选择主要分为监督学习与无监督学习,其中监督学习主要对描述符数据执行如回归、分类等任务[49]。回归任务可构建一个将训练集输入变量与输出变量相关联的模型,实现对测试集MOFs的性能预测[5]。这类算法包括:最小绝对值收敛和选择算子算法(Least Absolute Shrinkage and Selection Operator,LASSO)、线性回归(Linear Regression,LR)、核岭回归(Kernel Ridge Regression,KRR)、人工神经网络、深度学习(Deep Learning,DL)等。分类任务则根据输出变量将数据集分类为子集,确定描述符对应的取值范围及测其性能分类标准[5]。常见的分类算法包括:决策树(Decision Tree,DT)、随机森林(Random Forest,RF)、支持向量机(Support Vector Machines,SVM)、贝叶斯优化(Bayesian Optimization,BO)等。无监督学习主要用于探究尚未明确的关系与性能参数,如构效关系,包括K值聚类(K-means Cluster)、主成分分析(Principal Component Analysis,PCA)与奇异值分解(Singular Value Decomposition,SVD)。在机器学习辅助高通量筛选的研究中,也有衍生出的其他算法,以下介绍常用算法的基本原理,并于图4做简要展示。
图4 机器学习算法原理图

Fig. 4 Diagram of Machine learning algorithm

2.2.1 多元线性回归

多元线性回归[50](Multivariate Linear Regression,MLR)适用于预测大规模、多因素间存在线性关系的体系。在相互作用较弱的吸附模型中,MOFs性质与其性能间也是多因素相互影响,如饱和吸附量与孔容呈现线性相关[4],因而被广泛采用。

2.2.2 K近邻

K近邻算法[51](K-Nearest Neighbor,KNN)是通过测量“训练集”中不同特征值之间的距离进行分类与回归的算法。在MOFs数据库中,存在大量性质相似的结构,可采用此算法分类并预测其性能。

2.2.3 决策树

决策树[52]是一种传统的监督学习方法,是根据测试集中数据的属性,类比与“树枝结构”建立决策模型,定量地给出MOFs结构特征与性能之间的关系,但决策树算法不适合处理大规模数据和连续变量[4]。增强决策树[53](Boosted Decision Tree,BDT)则通过创建集成树模型,以循序渐进的方式构建每个回归树,并采用损失函数来衡量预测误差,进而提高DT的精度。

2.2.4 随机森林

随机森林[54]是决策树算法的扩展。通过训练集构建多个决策树并将其组合平均,实现更为准确的预测。

2.2.5 支持向量机

支持向量机[55]是一种数据分类导向方法, 它可以通过数学变换方法将数据集中的结构按一定规律区分开, 适合复杂线性或非线性构效关系, 比DT和KNN 算法更具灵活性, 往往能够获得更准确的预测结果,应用最广。此外,最小二乘支持向量机[56](Least Square Support Vector Machine,LSSVM)是在复杂系统中预测参数与建模最常用的方法之一。

2.2.6 神经网络

人工神经网络算法是为了找出各项结构特征与性能之间的联系,构建神经网络, 通过不断调节隐含层中的函数参数,得到一个适合的模型来准确预测测试集的性能。神经网络衍生的算法繁多,包括深度神经网络[57](Deep Neural Networks,DNN)、循环神经网络[58](Recurrent Neural Network,RNN)、反向传播神经网络[59](Back Propagation Neural Network,BPNN)等都已用于筛选高性能MOFs间的研究中。

2.2.7 进化算法

进化算法[60]主要包括基因遗传算法(Genetic Algorithm,GA)、进化策略(Evolution Strategies,ES)和进化规划(Evolution Programming,EP)。GA[61]是一种随机全局搜索并寻找最优解的算法,类似自然界中基因遗传的规律,新结构由上一代高性能的材料的基因遗传而来,在多代以后,能够预测出具有较高性能的MOFs 结构或发展出设计策略。

2.2.8 模型评估参数

评估回归机器学习模型预测精度主要通过以下参数:(1)绝对误差(Mean Absolute Error,MAE);(2)均方误差(Mean Square Error,MSE);(3)均方根误差(Root-Mean-Square Error,RMSE);(4)平均绝对比例误差(Mean Absolute Percentage Error,MAPE);(5)决定系数(R2);其中,n为数据集中样本数量,xi为模型输入的描述符数据,yi为模型输出的预测值, y ¯为预测数据的平均值[20]。一般而言,优秀的回归模型,其MAE、MSE、RMSE与MAPE接近0,R2接近1。而评估分类机器学习算法模型精度的参数则包括:(1)准确率(Accuracy,ACC),其中,TP为真正例,FP为假正例,TN为真反例,FN为假反例;(2)受试者工作特征(Receiver Operating Characteristic,ROC)下方的面积大小(Area Under the Curve,AUC)。ACC与AUC接近1,表明分类准确。值得一提的是,回归评价指标也可以用于分类算法预测评价。
M A E ( x , y ) = 1 n ∑ i = 1 n | x i - y i |
M S E ( x , y ) = 1 n ∑ i = 1 n | ( x i - y i ) 2
R M S E ( x , y ) = 1 n ∑ i = 1 n | ( x i - y i ) 2
M A P E ( x , y ) = 100 n ∑ i = 1 n x i - y i x i
R ( x , y ) 2 = 1 - ∑ i = 1 n ( x i - y i ) 2 ( y i - y - ) 2
A C C = T P + T N T P + T N + F P + F N
A U C ( x , y ) = 1 2 ∑ i = 1 n - 1 ( x i + 1 - x i ) ( y i + 1 + y i )

3 研究

3.1 气体储存

MOFs是由中心金属离子与有机配体连接而成的巨大晶格结构,它们可以形成一个具有高比表面积的三维网络[62]。这种多孔结构有助于吸附储存大量气体,包括氢气(H2)[63,64]、甲烷(CH4)[65]、二氧化碳(CO2)[66]、氮气(N2)[67]等。

3.1.1 H2储存

H2是一种理想的新能源燃料,广泛用于新能源汽车与燃料电池[68]等技术中,但面临着难以储存运输的问题。相比于低温压缩液态储氢,通过物理吸附储存氢气具有节能、安全等优势[68,69]。可通过调控MOFs与H2分子间的范德华力等参数,设计符合条件的MOFs实现高效储氢[70]。
表1简要总结了机器学习辅助筛选研发适用于H2储存MOFs的研究进展。其数据集主要来源于GCMC的高通量筛选结果,采用的描述符以能势信息为主,整体而言训练模型预测精度较高且构效关系明显。
表1 机器学习预测MOFs储氢性能

Table 1 The H2 storage performance of MOFs predicted by ML

Researcher Descriptors Algorithms Best Results
Cao[71] Geometrical + Chemical LSSVM, ANFIS, ANN R2 = 0.990, MAE = 0.050 wt%,
MSE = 0.059 wt%
Bucior[73] Energy-based LASSO R2 = 0.960, MAE = 2.40 g/L,
RMSE = 3.10 g/L
Giappa[74] Energy-based KRR, RFR, SVR MAE = 1.160×10-4 Ha
Ahmed[75,76] Geometrical DT, RF, LR, SVM, ERT, etc. R2 = 0.997, MAE = 0.10 wt%,
RMSE = 0.180 wt%
Cao等[71]训练了3大类机器学习算法,包括最小二乘支持向量机、自适应神经模糊系统(Adaptive Neuro-Fuzzy Inference System,ANFIS)、人工神经网络。采用“三步法”(试错法、精度分析法与排序法)策略,基于Spearman与Pearson[72]相关系数分析了各特征对MOFs储氢能力的影响,发现表面积与吸附焓是对MOFs储氢性能影响最大的描述符。ANN模型预测精度最高,其R2达0.99,且 MAE与MSE仅为0.05 wt%和0.059 wt%。
Bucior等[73]使用MOFs孔隙内势能面的能量特征作为描述符,采用基于特征选择与正则化的LASSO算法预测储氢能力。此描述符将H2作为探针分析MOFs网格化后的势能,进一步将能量分布简化为直方图,其每个子集都对应回归模型中的一类特征,预测MOFs结构中各空间的氢气吸附性能。以此方法对2250种hMOFs的数据库进行了交叉验证训练,在1000种hMOFs训练集的结果为:MAE=2.3 g/L,RMSE=3.0 g/L,R2=0.96;1250种hMOFs测试集的结果为:MAE=2.4 g/L,RMSE=3.1 g/L,R2=0.96。表明此模型预测H2吸附量的误差可控制在3.0 g/L以内,而计算速度仍比GCMC模拟快1000倍以上。并且,他们采用此方法从50 000种eMOFs中发现了MFU-4l,其储氢量高达47 g/L。
Giappa 等[74]首先采用ab-initio计算了氢气与58种C6H5-X(X为不同类型的官能团)的成键强度,发现—OCONH2、—SO2NH2、—OPO3H2、—OSO3H这四种官能团相互作用最强。其中,—OSO3H基修饰的成键强度与苯相比提高了80%。而后将IRMOF-8、IRMOF-16、IRMOF-14用这4种官能团修饰后进行GCMC模拟,在77 K与300 K的变压(0 bar ~ 100 bar)工况下获得吸附曲线,作为机器模型的训练数据集。使用库仑矩阵(Coulomb Matrix)、键袋(Bag of Bonds)、与原子势(Smooth Overlap of Atomic Potentials)作为描述符,训练了核岭回归、随机森林与支持向量机模型预测MOFs与H2的相互作用强度。结果中RF算法预测精度最高,在三类描述符下其MAE分别为1.99×10-4 Ha、1.16×10-4 Ha和2.10×10-4 Ha。
Ahmed等[75]将DT、LR、RF等14种算法组合后预测MOFs的储氢量。采用GCMC获得98,695种MOFs的H2等温吸附曲线作为数据集,以ρ、Va、GSA、SA、VF、LCD与PLD此7项结构特征为描述符,预测了918 734种MOFs在变压(5 bar ~ 100 bar)、变温变压(77 K、298 K)工况下的吸附质量与吸附容量。其中,极端随机树(Extremely Randomized Trees,ERT)模型脱颖而出,以变压工况的吸附质量为例,其R2达0.997,且MAE与RMSE仅为0.10 g/L、0.18 g/L。进一步的分析表明孔容与孔隙率为其中最为重要的描述符。采用此算法共识别出8282种储氢性能超过最佳纪录的hMOFs,均具有密度低(< 0.31 g/cm3)、比表面积高(> 5300 m2/g)、孔隙率(~ 0.90)与孔体积大(> 3.3 cm3/g)的特点。此工作是机器学习辅助筛选适用于H2储存的MOFs数据量最为丰富的研究,且模型展示于官方网站(https://sorbent-ml.hymarc.org)中,用户输入MOFs的结构数据后可快速获得其储氢性能[76]。

3.1.2 CH4储存

天然气是传统化石燃料到可再生能源的过渡燃料,其污染相对较低。通常,天然气中含有70% ~ 90%的CH4,是所有碳氢化合物中的燃烧能量最高的组成,需采用吸附等方式储存[77]。
CH4储存方面的研究如下表2所示,因为CH4为非极性分子,与MOFs相互作用较为简单,仅采用几何参数与化学信息作为描述符便可准确预测,且此体系里采用衍生算法较多。
表2 机器学习预测MOFs储甲烷性能

Table 2 The CH4 storage performance of MOFs predicted by ML

Researcher Descriptors Algorithms Best Results
Pardakhti[79] Geometrical + Chemical RF R2 = 0.980, MAPE = 7.180 cm3/g
Wang[80] Geometrical Graph Convolution Neural Networks (GCNN) AUC = 0.978 cm3/ cm3
Beauregard[78] Geometrical + Chemical RF, GA R2 = 0.950, MAPE = 1.370 cm3/g
Fanourgakis[81] Geometrical + Topological RF R2 = 0.990, RMSE = 9.050 cm3/g
Kim[82] Geometrical + Chemical SVM, DT, RF R2 = 0.947, MSE = 0.918 kJ/mol,
MAPE = 3.903 kJ/mol
Gurnani[19] Geometrical + Chemical Feed-forward Neural Networks R2 = 0.990, RMSE = 7.830 cm3/g
Suyetin[20] Geometrical MLR R2 = 0.990
Lee[83] Topological MSGA-FA *
Taw[84] Geometrical + Chemical BO R2 = 0.960
Suyetin[20]仅使用ASA、Va与ρ作为描述符,训练MLR模型预测CH4总吸附量与工作吸附量。其在预测 Nbo拓扑结构MOFs时R2=0.979(298 K),R2=0.987(273 K),R2=0.990(240 K);预测CoRE MOFs时R2也可达0.899,MAE与RMSE为9.23 cm3/g、12.60 cm3/g。Beauregard等[78]将基因遗传算法与随机森林算法结合构建了GARF算法,主要流程为采用GA构建了200条携带结构特征的“染色体”,在“种群”规模为100的情形下,迭代进化2000次后预测甲烷储存性能最优的MOFs,并结合RF预测每一代中的性能。将130 398种hMOFs数据按照1∶9的比例训练模型,筛选出了15种性能优异的MOFs,其甲烷吸附量最高达 414 cm3/g,R2=0.95,MAPE=1.37 cm3/g。Taw等[84]将MOFs的性能、金属团簇、有机配体与官能团编码后用于贝叶斯优化算法,将其拆分为结构相关部分与个体特征相关部分。而后采用与结构相关部分进行线性回归,同期将个体特征结合高斯过程(Gaussian Process,GP)形成LR + GP模型。两种模型均使用20种相同的MOFs作为贝叶斯优化的起点,每一次迭代增加一种由采样函数指定的训练集材料,可以发现在35 bar下,LR + GP模型能更快搜寻到性能优异的结构。以此方法训练457 000种hMOFs结构,仅需0.1%的数据作为输入,也能可靠地发现性能前20的结构。
在另一项研究中,Kim等[82]构建了一个蒙特卡洛机器学习(MC-ML)模型,预测4951种CoRE MOFs的甲烷吸附性能。与上述研究大多数基于GCMC模拟获取描述符数据不同的是,该工作收集实验中孔容、等温吸附曲线等数据作为输入,致力于预测其他工况下的吸附曲线。在采用的四种算法:线性支持向量机(Linear SVM)、非线性支持向量机(Nonlinear SVM)、决策树、随机森林中,RF在308 K和318 K下预测精度最高,其R2=0.947,MSE=0.918 kJ/mol,MAPE=3.903 kJ/mol。
研究人员从机器学习建模步骤中的特征转化获得启发,不直接将几何参数、拓扑结构、化学性质等描述符作为模型输入,而是通过数据处理形成全新的描述符。如Lee等[83]利用648个节点构造块(Node Building Blocks,NBBs)、219个边缘构建块(Edge Building Blocks,EBBs)与1775种拓扑结构开发了多孔材料构造器(pormake),生成了一个约有247万亿种hMOFs的数据库,并基于此构建了MOF-NET模型,采用深度学习算法探索最佳甲烷储存结构。如图5所示,通过将拓扑单元映射为随机的初始向量,在训练过程中对该向量进行迭代,将此结果放入多物种遗传算法(Multispecies Genetic Algorithm With Fitness Approximation,MSGA-FA)中筛选。结果显示,数据库中有964种hMOFs的CH4储存性能大于200 cm3/cm3,其中96种材料超越了甲烷储存纪录(208 cm3/cm3)。
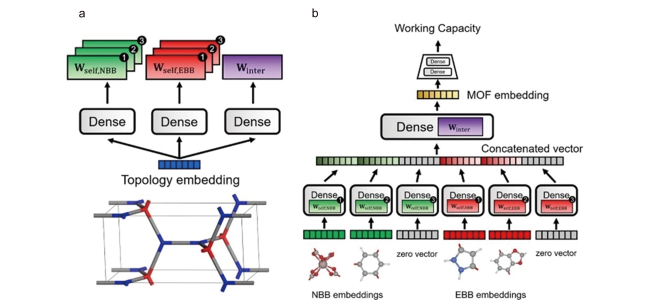
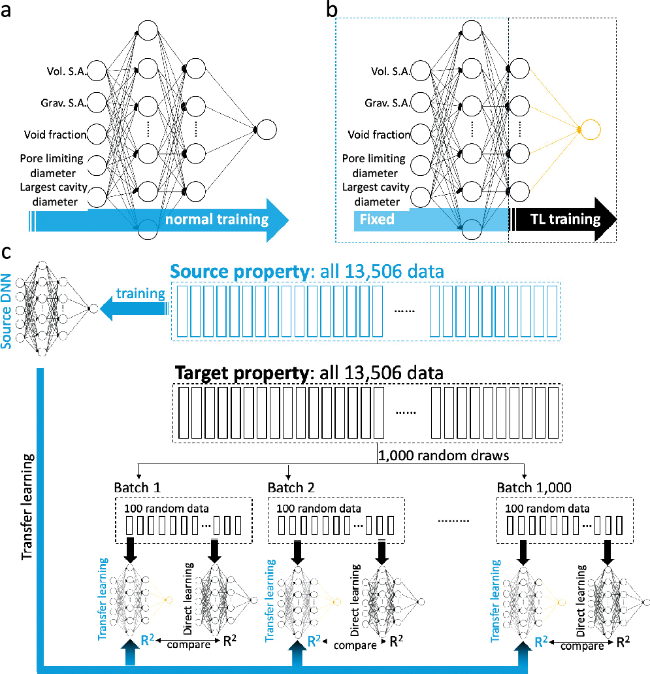
图5 MOF-NET模型图。“Dense”代表全连接层。(a)拓扑嵌入与拓扑嵌入权重的产生。Wself,NBB代表NBBs自身相互作用产生的权重,Wself,EBB代表EBBs自身相互作用产生的权重,Winter 代表相互作用产生的权重。(b)MOF-NET模型主要组成部分。模型由简单的全连接层组成,但某些层的权重由拓扑嵌入[83]

Fig. 5 Schematics of the MOF-NET architecture. The word “Dense” refers to fully connected layers. (a) Topology embedding and the generated weights from topology embedding. Wself,NBB is the self-interaction weight for NBBs, Wself,EBB is the self-interaction weight for EBBs and Winter is the interaction weight. (b) Main architecture of MOF-NET. The MOF-NET consists of simple fully connected layers, but the weights of some layers are generated from the topology embedding[83]

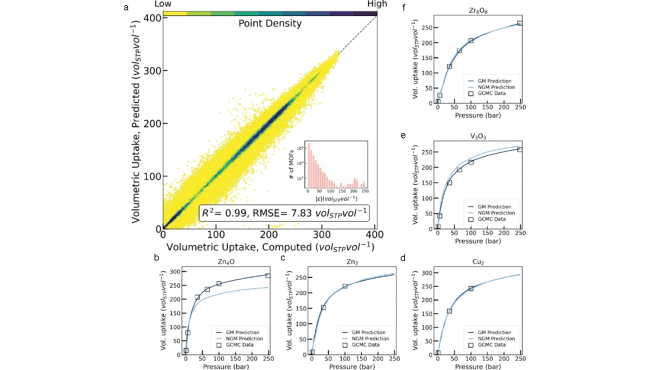
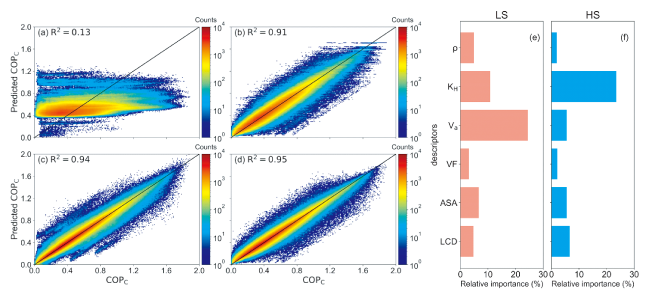
Gurnani等[19]训练了Gravimetric Uptake Model(GUM)、Geometric Model(GM)与Non-GM(NGM)三种模型预测137 953种hMOFs吸附甲烷性能。将30%数据设为测试集,并采用自上而下的方法移除权重较低的化学描述符,前馈神经网络将有效描述符映射预测结果。在298 K、35 bar下GUM模型预测的R2=0.99,RMSE=9.05 cm3/g。进一步地,对GM与NGM模型采用k-Fold交叉验证预测甲烷吸附曲线。区别在于NGM模型中去除了几何描述符,如图6所示,最终GM模型的R2=0.99,RMSE=7.83 cm3/g,NGM模型的R2=0.95,RMSE=18.64 cm3/g。NGM模型的高精度节省了大量计算几何描述符的成本,为筛选高性能MOFs提供了一种快捷的方法。
图6 (a) GM模型预测的533 430种CH4体积吸附量结果;(b~f) 示例结构中GM、NGM与GCMC预测吸附曲线结果对比[19]

Fig. 6 (a) Computed volumetric methane uptake vs predicted volumetric methane uptake for each of 533 430 measurements in the curated hMOFs data set;(b~f) NGM and GM predicted isotherms (light-blue and dark-blue curves, respectively) vs GCMC data (white squares) for five randomly selected MOFs[19]

3.1.3 碳捕捉

随着化石燃料被广泛使用,大量CO2被排放到大气中,引起了温室效应等问题。因此,使用MOFs吸附捕捉CO2成为了前沿研究热点[85].
近年来,机器学习辅助筛选适用于CO2吸附的MOFs进展如表3所示, 开发了多种晶体结构内原子分布位置的描述符。
表3 机器学习预测MOFs的分离性能

Table 3 The separation performance predicted by ML algorithms

Separation system Researcher Algorithms Descriptors
Noble gas Xe/Kr Liang[92] Ridge, LASSO, Elastic NET, SVM, Bayesian, ANN, RF, XGB Geometrical
Xe/Kr Ma[93] DNN Geometrical
Ar/Xe/Kr Anderson[94] DNN Geometrical + Topological
Xe/Kr Liu[95] BPNN Chemical
Cx/Cy ethane/ethylene Halder[96] RF Geometrical + Chemical
ethane/ethylene Wu[97] LR, DT, RF, SVM, KNN, GBT Geometrical + Chemical
C4/C7 Tang[98] MRGP Geometrical + Chemical
p-xylene/m-xylene/o-xylene Qiao[99] BPNN, DT Geometrical
Other CH4/H2S Cho[100] RF Geometrical + Chemical
N2/O2 Yan[101] RF, GBT, XGB Geometrical + Chemical
D2/H2 Zhou[102] SVM, RF, GBT, DNN Geometrical + Chemical
使用MOFs吸附含水条件下变压捕捉CO2往往较为困难,Deng 等[22]使用GCMC、MD模拟与反向传播神经网络(BPNN)、随机森林(RF)、决策树(DT)、支持向量机(SVM)四种机器学习方法研究CO2在CoRE MOFs中的吸附与扩散性能。发现RF模型预测吸附选择性的精度最高,其R2=0.981。结合多变量分析得到各描述符重要性的排序为:Qst > ρ > LCD > SA ≥VF > PLD,并最终获得了包括REYCEF、JAHNEM在内的14种碳捕捉性能优异的CoRE MOFs。
特征转化也被用于构建预测MOFs碳捕捉性能的机器学习算法模型中,Burner等[21]基于DNN构建了一个深度学习模型,用于预测在低压环境下(0.15 bar CO2,0.85 bar N2)材料的CO2吸附性能及CO2/N2的选择性。他们使用了34万种MOFs结构进行训练,以7∶1:2的比例分为训练、验证与测试集,以6种几何描述符(如SA、ρ等)、原子袋(The-bag of Atoms,BOA)、化学基序密度(Chemical Motif Density,CMD)、原子性质加权径向分布函数[89] (Atomic Property-weighted Radial Distribution Function,AP-RDF)作为模型输入。其中AP-RDF这一描述符最为关键,表示结构在给定距离内找到成对原子的概率分布。以此预测吸附量的结果R2 =0.965,RMSE=0.13 mmol/g,选择性为R2=0.975 mmol/g,RMSE=10 mmol/g。Fanourgakis等[81]使用探针原子被吸附概率作为模型的描述符,构建了一个预测纳米材料吸附CO2、H2与H2S含偶极矩分子的RF模型。单个粒子被多孔材料吸附的概率由平均玻尔兹曼因子求出,不同直径的探针原子(2.5 Å、3 Å、3.5 Å、4 Å)对每种MOFs的吸附概率是唯一的。模型将2932种CoRE MOFs按1∶2的比例分为训练集和测试集,结果表明具有小偶极矩的中性粒子(0.24 D)在模型中表现最优异,其R2=0.91 ~ 0.97。
机器学习算法也用于辅助设计新材料。Zhang等[87]结合蒙特卡洛树搜索法(MCTS)与递归神经网络算法研究了孔隙结构对材料碳捕捉性能的影响。从eMOFs中提取27种金属团簇和拓扑结构的信息作为输入,而后由MCTS生成一个有机链接器,通过重复选择、扩展、模拟、反向传播四个步骤形成节点以及蒙特卡洛树,一个节点对应一个简化分子线性输入规范[90](Simplified Molecular Input Line Entry System,SMILES)符号。在SMILES模型中,材料分子被表示为字符串序列,字符代表各种化学信息,如原子、键、环数、分支或离子等。利用RNN对SMILES模型进行训练,获得材料的有机配体,最终使用Zeo++设计出高性能MOFs,在 GCMC模拟中均具有良好的疏水性,可在潮湿环境下工作。且构效关系表明具有优异碳捕捉性能的MOFs孔径应稍小(如14.18 Å)、比表面积则应略大(如1750 m2/g)。

3.2 气体分离

气体吸附分离是MOFs研究的另一热点,尤其是在Cx/Cy、稀有气体与CO2捕捉分离等方面[91]。机器学习辅助的高通量筛选技术也是探究海量MOFs种类对于多元混合气体分离性能的重要手段。

3.2.1 稀有气体分离

放射性稀有气体在工业生产、生活各方面都有着特殊应用,目前采用低温蒸馏分离Xe/Kr等耗能巨大。而在MOFs分离稀有气体方面,其主要的特点在于稀有气体与MOFs间相互作用以范德华力为主,因而大部分机器学习工作仅以结构特征为描述符,如表4所示。Liang等[92]首先采用GCMC获得了303 991种GMOFs的Xe/Kr气体分离性能,采用LCD、PLD、Global cavity diameter(GCD)、Va、ρ、SA、VF为描述符,测试Ridge、LASSO、Elastic NET、SVM、BO、ANN、RF与XGB(Extreme Gradient Boosting)这些算法的预测性能。发现3∶7训练测试集比例时,XGB算法预测其吸附量和选择性的R2达0.951与0.973。并且识别出8种MOFs的分离性能优于Z11CBF-1000-2,38种MOFs选择性高于SBMOF-1,最高值为27.68。训练结果表明ρ、VF、Va、PLD权重高于其他描述符,对预测分离性能影响更为重要。
表4 机器学习预测MOFs储二氧化碳性能

Table 4 The CO2 capture performance predicted by ML

Researcher Descriptors Algorithms Results
Burner[21] Geometrical + Topological DNN R2 = 0.975, RMSE = 10.0 mmol/g
Dashti[86] Geometrical + Chemical PSO-ANFIS, RBF-ANN,
DE-ANFIS, LSSVM		 R2 = 0.997, MSE = 0.167 mmol/g
Deng[22] Geometrical + Chemical BPNN, RF, DT, SVM R2 = 0.994
Zhang[87] Chemical + Topological RNN, MCTS *
Li[88] Chemical SVM, KNN, DT, SGD, NN R2 = 0.940
Ma等[93]开发了基于迁移学习的深度神经网络,如图7所示,其理念为训练后将输入层与隐含层参数固定,不同体系下改变隐含层与输出层的关系。以SA、GSA、VF、LCD、PLD作为描述符,100 bar,243 K下的13 506例数据训练DNN模型,而后迁移学习预测H2、CH4的吸附量的R2为0.991和0.980,而预测Xe/Kr分离选择性的R2为0.092。说明基于结构性质描述符时,难以将其他气体训练得到的模型迁移用于Xe/Kr分离体系。Anderson等[94]则是基于多层感知器(Multilayer Perceptron,MLP)的深度学习模型,采用VF、GSA、LCD、PLD与PSSD(Pore Size Standard Deviation)作为描述符,预测了51 520种hMOFs的Ar、Kr、Xe、N2、CH4的单相吸附量,其MDAPE分别控制在9.0%、9.8%、11.1%、7.8%、9.4%与10.4%。而后结合理想吸附溶液理论[103](Ideal Adsorbed Solution Theory,IAST)预测Ar/Kr、Kr/Xe、CH4/C2H6与N2/CH4分离性能,发现此方法识别出Top 50结构中的21例(Xe/Kr),表明机器学习预测单相吸附性能后结合IAST可以评估混合相分离性能,但仍需进一步改进。
图7 DNN训练流程图:(a)一般流程; (b)迁移学习流程[93]

Fig. 7 Schematic diagrams for training DNN: (a) normal process; (b) transfer learning process[93]

Liu等[95]引入有机配体原子半径、电负性、配体空间、极化率等化学信息作为描述符,训练了BPNN模型预测Xe/Kr的吸附量、选择性、分离潜力、吸附性能参数,将GCMC获得的数据依据7∶1.5∶1.5分为训练、验证与测试数据集。不同体系下其预测R2均在0.94 ~ 0.98之间,且发现其中有机配体的长度权重最高,约为58.2%。因而纳入更多含化学信息的描述符,提高模型的泛化能力仍是发展方向。

3.2.2 Cx/Cy分离

类比于分子筛,MOFs在化工过程中潜在的应用便是诸如同系物与共沸物的Cx/Cy组分分离[104]。如表4所示,最近的研究主要集中于以结构特征与化学信息组合为描述符,采用监督学习算法预测乙烷/乙烯等体系的分离性能。Halder等[96]采用ρ、ASA、LCD、PLD四种结构性质与原子类型、数目等18项化学信息描述符,以8∶92比例分割数据集,训练RF预测115 302种hMOFs在298 K、1 bar下的乙烷/乙烯选择性,其预测精度R2约为0.89,并且发现VF是权重最高的描述符。Wu等[97]采用结构(ρ、GSA、SA、Va、PLD、LCD)与配体缺陷比例及化学信息(原子数目、金属团簇不饱和度与Zr元素比例)作为描述符,10-Flod交叉验证,以8∶2的训练测试集比例,对比线性回归、决策树、随机树森林、支持向量机、K近邻回归与梯度提升树(GBT)等算法在预测各类缺陷UiO-66的乙烷/乙烯的亨利系数、吸附热、工作吸附量、弹性模量与剪切模量等性质的差异。发现LR预测精度较高,R2接近1,且其中亨利系数(KH)描述符最为重要,其在1.0 bar工况下权重接近40%,其后则是GSA(23.5%)、TDU(15.5%)、DUC(8.9%)及Zr比例。如图8所示,由此提出了导向乙烷/乙烯分离目标吸附剂的路径,即GSA ≤ 1153.4 m2/g、Va ≤ 0.54 cm3/g、PLD ≤ 5.5 Å、LCD ≤ 8.7 Å的结构有84.2%的概率满足性能需求。
图8 UiO-66-Ds设计的决策树的原理图[97]

Fig. 8 Schematic of decision tree model for design of UiO-66-Ds[97]

在其余分离体系中,Tang等[98]以6种MOFs对66对近共沸物(C4、C7)的GCMC模拟结果为训练数据集,采用常用结构性质以及化学信息等25类描述符,预测了多达98种MOFs的分离性能。研究发现仅采用多元基因遗传算法(MRGP)时,在低压时、吸附量较低区域误差偏大,而通过结合机器学习与IAST模型,可以有效降低此误差。Qiao等[99]则仅基于VF、ASA、LCD、PLD与ρ这些结构特征,采用BPNN与DT预测了对二甲苯、间二甲苯与邻二甲苯的分离性能。其中BPNN在各工况下预测的R2均在0.9以上,MAE约为0.26,且发现PLD与LCD两种描述符权重最高,为0.37与0.28,其余均在0.12 ~ 0.16之间,表明了孔道对于分离的重要影响。

3.2.2 其他气体分离

在其他气体分离方面,Cho等[100]则也基于RF算法预测了CoRE-MOFs的CH4/H2S分离性能,发现将结构特征与金属元素键角、电荷、偶极矩等化学信息相结合,可以将预测的RMSE从 0.3降低至0.1。Yan等[101]采用LCD、VF、SA、PLD、ρ、KH、Qst作为描述符,按照7∶1.5∶1.5的训练集、验证集与测试集比例,训练了RF、GBT、XGB模型预测6013种CoRE MOFs在1 bar、298 K下的O2/N2的分离性能,包括选择性、工作吸附量、再生性能与吸附性能。XGB预测的平均R2为0.93,略高于GBT(0.92)和RF(0.91),且发现KH权重最高,其位于1.2 ~ 3.2 ×10-6 mol/kg/Pa区间时,分离性能最优。Zhou等[102]采用SVM、RF、GBT和DNN算法,在17-Fold交叉验证下,预测12 723种CoRE MOFs的D2/H2分离性能,发现在PLD、LCD和VF描述符中添加金属元素种类后,DNN模型提升最大。整体而言,SVM最佳,分析表明LCD应该略大于D2的尺寸,发挥动力学量子筛分KQS分离效应。而PLD与H接近时会出现排斥现象,需协同优化各类结构特征以达到最优性能。
在此类机器学习研究中,混合相气体分离较为复杂,因而结构性质与化学信息描述符已经被普遍采用。但仍需更进一步地开发新型描述符及算法提高预测的精度与模型迁移性。

3.3 MOFs理化性质

3.3.1 吸附式热泵

吸附式热泵[105](Adsorption-driven Heat Pumps,AHPs)是一种通过吸附剂与吸附质(工作流体)之间的吸脱附实现能量转换的新装置,因其节能、环保的特点得到了广泛的关注。
Li等[106]预测了乙醇/CoRE-MOFs工质对在单级和级联系统中的能效比(Coefficient of Performance,COP),首先采用PCA分析发现孔径是影响其性能的因素。决策树表明低温级工作吸附量 > 0.18 g/g是系统COP大于1.6的必要条件。而后[107]使用四种ML算法(MLR、DT、GBM和RF)预测评估了300多万种级联AHPs的COP(图9所示)。在引入了亨利系数作为化学描述符的情况下,采用20%数据作为训练数据集对比了四种算法。发现其中,RF的预测精度最高(R2=0.95),DT与GBM算法与之接近,而MLR的算法预测效果最差。并且分析表明Va是低温级描述符中影响COP的主要因素,而亨利系数是高温级中决定COP的关键因素。
Shi等[34]使用四种ML模型(BPNN、DT、RF和SVM)预测6013种甲醇/CoRE-MOFs工质对在热泵应用中的性能。以六类描述符(ρ、Qst、LCD、VF、SA和PLD)作为输入。精度最高的算法也为RF(R=0.86),其次则是BPNN(R=0.84),进一步分析得到了描述符的权重,与单变量分析结果一致,Qst和ρ是较为重要的描述符。DT阐明了导向高性能MOFs的路径(ρ < 885.10 kg/m3,Qst > 42.16,ϕ < 0.74 )。而后,Shi等[108]于2021年研究了6013种CoRE MOFs工质对在热源温度分别为355 K、365 K下三种工况(热泵、制冷及制冰)中的COP。通过单因素变量分析发现性能优异的结构其描述符聚集于ρ=434 ~ 1582 kg/m3、Qst=34 ~ 35 kJ/mol、LCD=7.0 Å ~ 22.0 Å、VF=0.65 ~ 0.90、SA=1550 ~ 3000 m2/cm3区间内。以此作为定向筛选的条件,发现137,953种hMOFs中筛选而得的结构有近80%满足以上条件。同时,他们采用公式8分析了MOFs工质对在AHPs中应用的经济性,Ctotal表示总成本,Cequipment表示设备成本,Ccycle表示循环消耗成本,CMOF表示材料成本。随着新型高性能MOFs材料的研发,Cequipment 所占比例下降而Ccycle逐渐增加,且进一步研究表明可通过提高Ccycle等手段降低Ctotal。此外,他们训练了6种机器学习算法:KRR、BPNN、SVM、DT、RF和梯度增强回归树(Gradient Boosting Regression Trees,GBRT)对Ctotal 进行预测,其中RF预测精度最高,其测试集结果为R=0.876,MAE=0.166,RMSE=0.262。且研究发现MOFs的金属类型描述符对AHPs的经济性影响较低,而Qst和ρ则影响显著。最后,他们实验中合成验证了一类MOF材料——DOTSOV03的经济成本,与模拟结果相一致,低至1 $/kJ。
C t o t a l = C e q u i p m e n t + C c y c l e + C M O F
图9 (a)MLR,(b)DT,(c)GBM 与(d)RF算法预测3 166 602种级联工质对在吸附式热泵中的COPC,(e)低温级与(f)高温级描述符权重[106]

Fig. 9 COPC predicted by varying machine learning models (a)MLR,(b)DT, (c)GBM, and(d)RF, colored by the number density of cascaded AHPs, weights of descriptors at low (e) and high (f) temperatures[106]

3.2 催化领域

MOFs自身良好的稳定性、孔隙率和周期性,使其在催化领域得到了广泛的应用[109]。设计新型催化剂需全面考虑各类因素,包括反应过程中的温度、压力、时间、pH值等。这些多元变量间的关系及其对MOFs催化性能的影响极其复杂。而结构性质对这些因素的反应也不尽相同,因此需深入研究其结构性质(如:表面积、孔径、孔隙率、电荷分配等)在不同条件下的催化性能[110]。
Liu等[95]总结了约100篇文献中采用MOFs催化二氧化碳固定为环状碳酸盐的数据。选定MOFs的金属团簇与有机配体、及CO2固定反应中的反应物与产物构造数据集,以8∶2比例训练了SVM、KNN、DT、随机梯度下降(Stochastic Gradient Descent,SGD)和ANN等多种ML算法预测MOFs催化二氧化碳的性能,并从精确度、召回率、F1分数(精确性和召回率的调和平均值)的角度来比较几种ML算法的优越性。结果发现SVM、SGD、ANN模型的精确度较高,其F1分数分别为0.92、0.93、0.92,而KNN、DT的精确度只有0.82、0.81。为了进一步提升训练模型的精确度,他们将SVM、SGD、ANN结合后迁移预测1311种hMOFs的催化性能,发现在CO2催化固定中最佳的金属离子为Mn、V、Cu、Ni、Zr和Y,相应的配体为TACTMB、TDCBPP、TCPP、H3L,推测这6种金属和4种配体结合成的24种MOFs在催化固定二氧化碳方面可能具有优异的性能。
Chen等[111]从粉晶X射线衍射与电子扫描显微镜(Scanning Electron Microscopy,SEM)的实验图像中提取相图和形态关系,训练了多元决策树(Multivariate Decision Tree,MDT)模型。并以9∶1的比例对高维合成空间的相边界进行预测,用SMOTE[112](Synthetic Minority Oversampling Technique)对数据进行平衡,从众多影响因素(温度、HfCl4、H2BPDC、DMF、H2O和HCO2H的浓度)中发现温度、H2O和HCO2H的浓度的影响最为显著。并将1000种不同的MDT构建为随机森林,在固定温度下以H2O和HCO2H的浓度作为描述符预测NMOFs(主要为UiO-67、hcp-UiO-67、hxl-UiO-67)的相分布,模型平均精度达到80%。随后,他们使用透射电子显微镜(TEM)和质谱(MS)观察MOFs合成溶液中的HF6与HF12SBUs(Secondary Building Units,SBUs)成分。证实了先形成SBUs,后在SBUs上交换基团,而后交联成固体网络的晶体生长机制。同时,通过研究相图和晶体形态及其生长条件之间的关系,发现在溶液中形成Hf12SBUs对确定晶体的相至关重要。为此,采用CNN模型对228幅SEM扫描图像的晶体厚度/长度进行训练,并对31幅标记后的图像进行了预测,R2为0.81,且长度和厚度的MAE分别为0.1和0.14。他们还发现hxl-UiO的厚度与横向尺寸随着溶液中SBUs浓度增加而提高,采用配体溶解度和调节剂浓度可定量预测特定形态下NMOFs晶体的生长情形,基于此原理可设计合成步骤来获得增强了基质传输的NMOFs,提升其催化烯烃加氢的反应活性。

3.3.3 稳定性

随着MOFs的应用领域的不断拓展,研究人员愈发关注其结构能否在实际应用环境下稳定。
Nandy等[113]收集了数千篇关于MOFs稳定性的文献数据,如图10所示,利用自然语言处理(Natural Language Processing,NLP)识别出CoRE-MOFs 数据库中2179种MOFs溶剂活化后的稳定性,及3132种结构在热重分析下的热稳定性。同步收集MOFs的晶体文件,整理出SBUs和有机配体,并使用Zeo++计算诸如孔径、比表面积、孔容与密度等信息。基于cif文件,由金属团簇中心原子或卟啉环中N原子的连接建立修正自相关函数,一并作为描述符,采用ANN预测收集结构的溶剂活化稳定性与热稳定性,其R2=0.76,AUC=0.79,热稳定性的MAE为47 ℃。而后进一步对MOFs的热稳定性进行了研究[114],加入基于聚类原理的高斯过程后,其AUC提升至0.81,MAE降低为44 ℃。
图10 为溶剂移除活化和热稳定性数据集整理流程[113]

Fig. 10 Workflows for curating datasets for solvent removal and thermal stability[113]

水稳定性是另一重点关注的性质。Batra等[115] 按照MOFs材料的水稳定性将其分为四类:稳定(Stable)、高动力学稳定(High Kinetic Stability)、低动力学稳定(Low Kinetic Stability)和不稳定(Unstable)。随后根据MOFs金属团簇、有机配体和金属-配体摩尔比这三种化学性质,使用递归特征消除法(Recursive Feature Elimination,RFE)降维优化特征,将二类和三类模型的 RFE 测试准确度分别从80%与64%提高到83%和71%。基于此两类特征,采用SVM、RF和GB三种机器学习模型在5-Fold交叉验证下训练预测207种MOFs的水稳定性,其二三类模型的R2为88%和71%。并以此预测另外10种MOFs的水稳定性,其二、三类的R2分别达0.9和0.6。使用二类RF模型分析构效关系,表明具有大原子半径(> 1.4 Å)与较低电离势(< 7.5 eV)金属原子,以及低六元环的数量(< 0.04)和高环状二价节点(> 0.01)配体的MOFs均具有较高水稳定性。

3.3.4 电化学性质

MOFs材料的电化学性质显著影响其在电催化、电阻传感与电极材料等领域的应用前景,而大部分MOFs结构因其高孔隙率与共价键/配位键连接导致其几近绝缘,因而研究者们开始深入探究MOFs的电化学性质,尤其是点电荷,以期重新设计或将其改性得到适宜的结构[116]。
Raza等[117]构建了消息传递神经网络 (Message Passing Neural Network,MPNN)模型。其训练、验证与测试集比例为7∶1∶2。以MOFs内原子的局部键合环境作为描述符预测各原子的点电荷。采用随机梯度下降方法对模型进行优化,发现超参数为r=4(元素嵌入维度)、k=10(隐藏节点特征维度)、t=30(消息传递时间步数)下模型预测效果最佳。基于此预测了 2266 种MOFs在DFT计算而得的电荷,其预测值与DDEC(Density Derived Electrostatic and Chemical)电荷的MAE为0.025,而该方法预测耗时约3 s,显著降低了计算成本。
Rosen等[46]采用几何形状、能量、带隙、电荷密度、状态密度、部分电荷、自旋密度和键阶等描述符预测了15 713种MOFs的导带。以8∶2比例分配数据集后训练了核岭回归、晶体图卷积神经网络、原子位置的平滑重叠模型,结果显示晶体图卷积神经网络模型预测效果最优,其R2=0.88,MAE=0.27 eV。此模型可预测出具有所需电子结构特性的 MOFs材料,筛选出低带隙的样本,以期获得高电导率的MOFs。最终,其发现Ag(DCl)2(DCl=2,5-Cl,Cl-N,N0-dicyanoquinone diamine)的带隙为0.71 eV,具有较高导电率;而高带隙的Sr[C2H4(SO3]2](带隙为8.36 eV)几近绝缘。Korolev等[118]等结合DDEC与Qeq电荷计算方法设计了梯度增强决策树(Gradient Boosting Decision Trees,GBDT)模型。以相应位点元素的内在性质(如原子序数、共价半径和溶解温度与相邻共价/配位环境的位置信息(如原子近邻数量、拓扑分布)作为描述符,采用9∶1比例分配训练集与测试集且在10-Fold交叉验证下训练GBDT模型预测CoRE MOFs中部分结构的电荷,与DDEC电荷对比,发现其预测的MAD低至0.01 e。MOFs和COFs中原子局部环境描述符的差别如图11所示,此条件下将该模型迁移用于CURATED COFs,预测精度仍然较高,MAD仅为0.05 e。此外,采用此方法计算得到在二氧化碳吸附特性模拟中,与DDEC电荷模拟的结果相一致,表明了该方法的有效性与高准确度。
图11 MOF和COF中原子的局部环境的描述符分布[118]

Fig. 11 Distributions of several illustrative ML descriptors used to represent the local environment of MOF and COF atoms[118]

Kancharlapalli等[119]采用原子属性(电负性、第一电离势)与其配位环境(相邻原子数、平均成键距离、成键原子平均电负性、成键原子平均第一电离势)等化学信息作为描述符,以8∶2比例在10-Fold交叉验证下训练了线性回归、神经网络、梯度增强决策树和随机森林四种模型预测10,143种CoRE MOFs 拥有ASR(All Solvent Removed)结构的DDEC电荷,RF训练精度达R2=0.9952,RMSE=0.0337,MAE=0.0192,预测CM5(Charge Model 5)电荷的精度更高,为R2=0.9969,MAE=0.010。采用这两模型预测了另外404种MOFs上的DDEC和CM5电荷,其R2分别为0.9899和0.9932,MAE为0.026和0.013,表明RF模型可适用于其他多孔晶体及分子筛的电荷预测。

3.3.5 其他

MOFs的实验比表面积通常使用气体吸附法(BET)计算而得。然而,对于比表面积较大的结构,该方法计算时可能会将非单层的吸附分子视为单层吸附(即孔隙填充污染问题),以致高估比表面积。Datar等[120]提出采用数据驱动的方法精确预测MOFs的表面积。他们基于328种MOFs的等温吸附曲线以4∶6的比例训练了LASSO模型,以预测其实际单层面积。研究发现该模型可以预测出绝大多数MOFs的真正单层面积,且偏差小于20%。仅有18种MOFs(5.5%)在该模型下预测偏差超过20%,但控制在30%以下,相较于BET方法更为准确。他们进一步模拟了68种MOFs的N2(77 K)等温吸附曲线。如图12所示,发现ML预测的真实单层面积偏差均在20%以下,而BET方法高估了其中20种材料的面积。且面积越大,则偏差越高,最高达到了77%。
图12 ML模型与使用 N2 等温线BET 方法(a)预测MOF实际单层面积结果与其(b)差异示意图[120]

Fig. 12 (a) Predicted areas and (b) schematic of deviation of the ML model compared to the BET method using N2 isotherms for true monolayer prediction[120]

Syah等[121]研究了由金属有机骨架和层状双氢氧化物(Layered Double Hydroxide,LDH)组成的复合材料Ni50Co50-LDH/UIO-66-NH2。以温度和吸附质(铊Tl)的初始浓度作为描述符训练了ANN模型,预测其溶液中重金属离子的平衡浓度,该模型预测的R2均大于0.999,且进一步分析发现溶液中Tl初始浓度对平衡浓度的影响较大,温度对平衡浓度的影响较小。

4 结论与展望

综上所述,机器学习辅助高通量筛选金属有机骨架材料在近年来发展迅猛。究其原因在于MOFs的数量呈现爆炸式增长的趋势,且其应用范围、条件不断拓展。而高通量筛选是目标导向的发现高性能目标MOFs、挖掘构效关系的主流方法。但筛选过程产生的数据量大,特征维度多,所耗计算资源显著,正与机器学习长短相补。两者结合如虎添翼,可高效、准确的研究MOFs的性质及其各类应用下的性能,深入阐明其构效关系,指导设计策略。
在描述符方面,现阶段的研究主要采用监督学习对MOFs材料进行筛选,该模型数据集的核心一般是各类具有标签的描述符。其中,几何参数与化学性质描述符较易获取,而拓扑结构与能势信息的描述符由于技术、时间与计算成本等因素获取难度较高,且标记标签的过程复杂,为训练监督学习模型带来了诸多困难。因此,需继续发展更多方便获取的描述符,增加模型输入特征与信息,以此提升机器学习模型性能,更为高效、精确的发现各类应用下的目标MOFs;另一方面,可通过开发其他机器学习算法:如半监督学习和无监督学习模型,在没有标签的数据集中,训练ML模型预测发现优异MOFs材料,但这可能需要更为海量的数据提供隐含关系、更高精度的机器学习算法精确发现材料以及其相匹配的实验验证策略。而在机器学习所采用的MOFs结构数据库方面,虽然目前机器学习模型预测精度较高,但几乎均是原数据库。尤其是训练预测CoRE MOFs等性能时,通常是基于树分类的算法性能较优,如RF等,可能导致模型泛化性能差。需进一步增强算法的迁移能力,例如以eMOFs训练的机器学习模型训练预测hMOFs,甚至是COFs、沸石(Zeolite)等其他多孔结构的性能。并且由于大多数机器学习模型具有的“黑匣子”特性[122],研究训练的机器学习模型通常仅停留在预测现有数据库中最优MOFs层面。因此,开发可选择、可优化与可解释的模型,如LR、DT、KNN等,从而直接推出新型高性能MOFs的设计策略,或明确揭示材料中各类隐含的关系特征,是机器学习未来发展的应有之义。
此外,模拟计算结果往往与实验合成具有差距,研究人员筛选出大量优异的hMOFs,实际实验结果中却可能不尽如人意。发展机器学习算法时若将实验与模拟中的差异因素,如溶剂活化、晶体缺陷等也作为描述符引入,从而可能减少此类误差。并且,机器学习算法与分子模拟虽结合于高通量筛选中,但目前大部分研究中仍然是相对独立的两个过程,一般是分子模拟结束后再采用机器学习分析预测。设想将机器学习深度融合于分子模拟或实验流程中,如某些参数可通过仅机器学习预测后嵌入分子模拟计算或实验设计流程中。总而言之,机器学习辅助高通量筛选MOFs仍然面临一些问题,但其在描述符获取、算法开发、模型应用等方面发展迅速,将是未来高效设计、研发MOFs中不可或缺的关键技术。

参考文献

原文顺序 | 文献年度倒序 | 文中引用次数倒序
[1]
Heidarinejad Z, Dehghani M H, Heidari M, Javedan G, Ali I, Sillanpää M. Environ Chem Lett, 2020, 18 (2): 393.

[2]
Van Speybroeck V, Hemelsoet K, Joos L, Waroquier M, Bell R G, Catlow C R A. Chem. Soc. Rev., 2015, 44 (20): 7044.

DOI PMID

[3]
Wang H J, Wang M D, Liang X, Yuan J Q, Yang H, Wang S Y, Ren Y X, Wu H, Pan F S, Jiang Z Y. Chem. Soc. Rev., 2021, 50 (9): 5468.

[4]
Liu Z L, Li W liu H, Zuang X D, Li S. Acta Chim Sinica, 2019, 77 (4): 323.

(刘治鲁, 李炜, 刘昊, 庄旭东, 李松. 化学学报. 2019, 77(4): 323.)

DOI

[5]
Altintas C, Altundal O F, Keskin S, Yildirim R. J Chem Inf Model, 2021, 61 (5): 2131.

[6]
Ahmed A, Seth S, Purewal J, Wong-Foy A G, Veenstra M, Matzger A J, Siegel D J. Nat. Commun., 2019, 10 (1): 1.

[7]
Herm Z R, Bloch E D, Long J R. Chem. Mater., 2014, 26 (1): 323.

[8]
Tan K, Zuluaga S, Gong Q H, Gao Y Z, Nijem N, Li J, Thonhauser T, Chabal Y J. Chem. Mater., 2015, 27 (6): 2203.

[9]
Zhao X, Wang Y X, Li D S, Bu X H, Feng P Y. Adv. Mater., 2018, 30 (37): 1705189.

[10]
Janiak C. J Eur. J. Inorg. Chem, 2012, 2625: 2634.

[11]
Li W, Xia X X, Li S. ACS Appl. Mater. Interfaces, 2019, 12 (2): 3265.

[12]
Chen L Y, Xu Q. Matter, 2019, 1 (1): 57.

[13]
Jiao L, Wang Y, Jiang H L, Xu Q. Adv. Mater., 2018, 30 (37): 1703663.

[14]
Lee J, Farha O K, Roberts J, Scheidt K A, Nguyen S T, Hupp J T. Chem. Soc. Rev., 2009, 38 (5): 1450.

[15]
Chu F L, Hu J L, Wu C L, Yao Z G, Tian J, Li Z, Li C L. ACS Appl. Mater. Interfaces, 2018, 11 (4): 3869.

[16]
Moghadam P Z, Li A, Wiggin S B, Tao A, Maloney A G, Wood P A, Ward S C, Fairen-Jimenez D. Chem. Mater., 2017, 29 (7): 2618.

[17]
Wilmer C E, Leaf M, Lee C Y, Farha O K, Hauser B G, Hupp J T, Snurr R Q. Nat. Chem., 2012, 4 (2): 83.

[18]
Colón Y J, Gomez-Gualdron D A, Snurr R Q. Cryst. Growth Des., 2017, 17 (11): 5801.

[19]
Gurnani R, Yu Z Z, Kim C, Sholl D S, Ramprasad R. Chem. Mater., 2021, 33 (10): 3543.

[20]
Suyetin M. Faraday Discuss., 2021, 231: 224.

[21]
Burner J, Schwiedrzik L, Krykunov M, Luo J, Boyd P G, Woo T K. J. Phys. Chem. C, 2020, 124 (51): 27996.

[22]
Deng X M, Yang W Y, Li S H, Liang H, Shi Z N, Qiao Z W. Appl. Sci., 2020, 10 (2): 569.

[23]
Islamoglu T, Idrees K B, Son F A, Chen Z, Lee S-J, Li P, Farha O K. J. Mater. Chem. A, 2022, 10 (1): 157.

[24]
Jain A K, Mao J, Mohiuddin K M. Comput., 1996, 29 (3): 31.

[25]
Friedman J H. Ann Appl Stat, 2001, 29 (5): 1189.

[26]
Pang B, Nijkamp E, Wu Y N. J Educ Behav Stat, 2019, 45 (2): 227.

[27]
Chen K M, Cofer E M, Zhou J, Troyanskaya O G. Nat. Methods, 2019, 16 (4): 315.

[28]
Pedregosa F, Varoquaux G, Gramfort A, Michel V, Thirion B, Grisel O, Blondel M, Prettenhofer P, Weiss R, Dubourg V. J Mach Learn Res, 2011, 12: 2825.

[29]
Chung Y G, Camp J, Haranczyk M, Sikora B J, Bury W, Krungleviciute V, Yildirim T, Farha O K, Sholl D S, Snurr R Q. Chem. Mater., 2014, 26 (21): 6185.

[30]
Li S, Chung Y G, Simon C M, Snurr R Q. J. Phys. Chem. Lett, 2017, 8 (24): 6135.

[31]
Sarkisov L, Bueno-Perez R, Sutharson M, Fairen-Jimenez D. Chem. Mater., 2020, 32 (23): 9849.

[32]
Dubbeldam D, Calero S, Ellis D E, Snurr R Q. Mol Simul, 2016, 42 (2): 81.

[33]
Kadioglu O, Keskin S. Sep. Purif. Technol., 2018, 191: 192.

[34]
Shi Z N, Liang H, Yang W Y, Liu J, Liu Z L, Qiao Z W. Chem. Eng. Sci., 2020, 214: 115430.

[35]
Adatoz E, Avci A K, Keskin S. Sep. Purif. Technol., 2015, 152: 207.

[36]
Altundal O F, Haslak Z P, Keskin S. Ind. Eng. Chem. Res., 2021, 60 (35): 12999.

DOI PMID

[37]
McDaniel J G, Li S, Tylianakis E, Snurr R Q, Schmidt J. J. Phys. Chem. C, 2015, 119 (6): 3143.

[38]
Zhong C L, Liu D H, Yang Q Y. Structure-Property Relationship and Design of Metal-Organic Frameworks. Beijing: Science Press, 2013. 35.

仲崇立, 刘大欢, 阳庆元. 金属-有机骨架材料的构效关系及设计. 北京: 科学出版社, 2013. 35.).

[39]
Keskin S, Liu J C, Rankin R B, Johnson J K, Sholl D S. Ind. Eng. Chem. Res., 2009, 48 (5): 2355.

[40]
Jiang J W, Babarao R, Hu Z Q. Chem. Soc. Rev., 2011, 40 (7): 3599.

[41]
Smit B, Maesen T L. Chem. Rev., 2008, 108 (10): 4125.

[42]
Düren T, Bae Y-S, Snurr R Q. Chem. Soc. Rev., 2009, 38 (5): 1237.

DOI PMID

[43]
Wang M, Wang T, Cai P Q, Chen X D. Small Methods, 2019, 3 (5): 1900025.

[44]
Oliynyk A O, Mar A. Acc. Chem. Res., 2018, 51 (1): 59.

[45]
Krishnapriyan A S, Haranczyk M, Morozov D. J. Phys. Chem. C, 2020, 124 (17): 9360.

[46]
Rosen A S, Iyer S M, Ray D, Yao Z, Aspuru-Guzik A, Gagliardi L, Notestein J M, Snurr R Q. Matter, 2021, 4 (5): 1578.

[47]
Ward L, Liu R Q, Krishna A, Hegde V I, Agrawal A, Choudhary A, Wolverton C. Phys. Rev. B, 2017, 96 (2): 024104.

[48]
Chong S, Lee S, Kim B, Kim J. Coord Chem Rev, 2020, 423: 213487.

[49]
Moreno-Torres J G, Sáez J A, Herrera F. IEEE Trans Neural Netw Learn Syst, 2012, 23 (8): 1304.

[50]
Chung M K, Worsley K J, Nacewicz B M, Dalton K M, Davidson R J. NeuroImage, 2010, 53 (2): 491.

DOI PMID

[51]
Zhang M-L, Zhou Z-H. Pattern Recognit, 2007, 40 (7): 2038.

[52]
Raccuglia P, Elbert K C, Adler P D, Falk C, Wenny M B, Mollo A, Zeller M, Friedler S A, Schrier J, Norquist A J. Nature, 2016, 533 (7601): 73.

[53]
Gligorov V V, Williams M. J. Instrum., 2013, 8 (02): P02013.

[54]
Belgiu M Dr?gu瘙塅 L. ISPRS J. Photogramm, 2016, 114: 24.

[55]
Cherkassky V, Ma Y. Neural Netw, 2004, 17 (1): 113.

[56]
Suykens J A, Vandewalle J. Neural Process Lett, 1999, 9 (3): 293.

[57]
Montavon G, Samek W, Müller K-R. Digit Signal Process, 2018, 73: 1.

[58]
Medsker L R, Jain L. Comput Aided Des Appl, 2001, 5: 64.

[59]
Erb R J. Pharm. Res., 1993, 10 (2): 165.

[60]
Angeline P J, Saunders G M, Pollack J B. IEEE Trans Neural Netw Learn Syst, 1994, 5 (1): 54.

[61]
Whitley D. Stat Comput, 1994, 4 (2): 65.

[62]
Sillar K, Hofmann A, Sauer J. J. Am. Chem. Soc., 2009, 131 (11): 4143.

DOI PMID

[63]
Bobbitt N S, Snurr R Q. Mol Simul, 2019, 45: 1069.

[64]
Ren J, Musyoka N M, Langmi H W, Swartbooi A, North B C, Mathe M. Int. J. Hydrog. Energy, 2015, 40 (13): 4617.

[65]
Maryam P, Ehsan M, David W, Suib S L, Ranjan S. ACS Comb Sci, 2017, 19 (10): 640.

[66]
Fernandez M, Boyd P G, Daff T D, Aghaji M Z, Woo T K. J. Phys. Chem. Lett, 2014, 5 (17): 3056.

DOI PMID

[67]
Fernandez M, Barnard A S. ACS Comb Sci, 2016, 18 (5): 243.

DOI PMID

[68]
Lin X, Jia J H, Hubberstey P, Schrder M, Champness N R. CrystEngComm, 2007, 9 (6): 438.

[69]
Getman R B, Bae Y S, Wilmer C E, Snurr R Q. Chem. Rev., 2012, 112 (2): 703.

[70]
Gangu K K, Maddila S, Mukkamala S B, Jonnalagadda S B. J. Energy Chem., 2018, 30 (03): 140.

[71]
Cao Y, Dhahad H A, Zare S G, Farouk N, Anqi A E, Issakhov A, Raise A. Int. J. Hydrog. Energy, 2021, 46 (73): 36336.

[72]
Jiang Y C, Zhang G F, Wang J J, Vaferi B. Int. J. Hydrog. Energy, 2021, 46 (46): 23591.

[73]
Bucior B J, Bobbitt N S, Islamoglu T, Goswami S, Gopalan A, Yildirim T, Farha O K, Bagheri N, Snurr R Q. Mol. Syst. Des. Eng., 2019, 4 (1): 162.

[74]
Giappa R M, Tylianakis E, Di Gennaro M, Gkagkas K, Froudakis G E. Int. J. Hydrog. Energy, 2021, 46 (54): 27612.

[75]
Ahmed A, Siegel D J. Patterns, 2021, 2 (7): 100291.

[76]
Glasby L T, Moghadam P Z. Patterns, 2021, 2 (7): 100305.

[77]
Martin R L, Simon C M, Smit B, Haranczyk M. J. Am. Chem. Soc., 2014, 136 (13): 5006.

[78]
Beauregard N, Pardakhti M, Srivastava R, Modeling. J Chem Inf Model, 2021, 61 (7): 3232.

DOI PMID

[79]
Pardakhti M, Nanda P, Srivastava R. J. Phys. Chem. C, 2020, 124 (8): 4534.

[80]
Wang R H, Zhong Y S, Bi L M, Yang M L, Xu D G. ACS Appl. Mater. Interfaces, 2020, 12 (47): 52797.

[81]
Fanourgakis G S, Gkagkas K, Tylianakis E, Froudakis G. J. Phys. Chem. C, 2020, 124 (13): 7117.

[82]
Kim S Y, Kim S I, Bae Y S. J. Phys. Chem. C, 2020, 124 (36): 19538.

[83]
Lee S, Kim B, Cho H, Lee H, Lee S Y, Cho E S, Kim J, Interfaces. ACS Appl. Mater. Interfaces, 2021, 13 (20): 23647.

[84]
Taw E, Neaton J B. Adv. Theory Simul., 2022, 5 (3): 2100515.

[85]
Zendehboudi S, Bahadori A, Lohi A, Elkamel A, Chatzis I. Energy Fuels, 2013, 27 (1): 401.

[86]
Dashti A, Bahrololoomi A, Amirkhani F, Mohammadi A H. J. CO2 Util., 2020, 41: 101256.

[87]
Zhang X Y, Zhang K X, Yoo H, Lee Y J. ACS Sustain. Chem. Eng., 2021, 9 (7): 2872.

[88]
Li S Y, Zhang Y J, Hu Y X, Wang B J, Sun S R, Yang X W, He H. J. Materiomics, 2021, 7: 1029.

[89]
Fernandez M, Trefiak N R, Woo T K. Journal of Physical Chemistry C, 2013, 117 (27): 14095.

[90]
Weininger D. J Chem Inf Model, 1988, 28 (1): 31.

[91]
Li J-R, Sculley J, Zhou H-C. Chem. Rev., 2012, 112 (2): 869.

[92]
Liang H, Jiang K, Yan T-A, Chen G H. ACS Omega, 2021, 6 (13): 9066.

DOI PMID

[93]
Ma R, Colón Y J, Luo T. ACS Appl. Mater. Interfaces, 2020, 12 (30): 34041.

[94]
Anderson R, Biong A, Gomez-Gualdron D A. J. Chem. Theory Comput., 2020, 16 (2): 1271.

DOI PMID

[95]
Liu Z W, Zhang K, Xia Q B, Wang X J, Huang B C, Xi H X. Chem. Eng. Sci., 2021, 243: 116772.

[96]
Halder P, Singh J K. Energy Fuels, 2020, 34 (11): 14591.

[97]
Wu Y, Duan H P, Xi H X. Chem. Mater., 2020, 32 (7): 2986.

[98]
Tang D, Gharagheizi F, Sholl D S. J. Phys. Chem. B, 2021, 125 (3): 926.

[99]
Qiao Z W, Yan Y L, Tang Y X, Liang H, Jiang J W. J. Phys. Chem. C, 2021, 125 (14): 7839.

[100]
Cho E H, Deng X P, Zou C L, Lin L-C. J. Phys. Chem. C, 2020, 124 (50): 27580.

[101]
Yan Y L, Shi Z N, Li H L, Li L F, Yang X, Li S H, Liang H, Qiao Z W. Chem. Eng. J., 2022, 427: 131604.

[102]
Zhou M S, Vassallo A, Wu J Z. J. Membr. Sci., 2020, 598: 117675.

[103]
Simon C M, Smit B, Haranczyk M. Comput Phys Commun, 2016, 200: 364.

[104]
Bao Z B, Chang G G, Xing H B, Krishna R, Ren Q L, Chen B L. Energy Environ. Sci., 2016, 9 (12): 3612.

[105]
De Lange M F, Verouden K J, Vlugt T J, Gascon J, Kapteijn F. Chem. Rev., 2015, 115 (22): 12205.

[106]
Li W, Xia X X, Cao M, Li S. J. Mater. Chem. A, 2019, 7 (13): 7470.

[107]
Li W, Xia X X, Li S. J. Mater. Chem. A, 2019, 7 (43): 25010.

[108]
Shi Z N, Yuan X Y, Yan Y L, Tang Y L, Li J J, Liang H, Tong L P, Qiao Z W. J. Mater. Chem. A, 2021, 9 (12): 7656.

[109]
McCarver G A, Rajeshkumar T, Vogiatzis K D. Coord Chem Rev, 2021, 436: 213777.

[110]
Erdem Günay M, Yıldırım R. Catal Rev Sci Eng, 2021, 63 (1): 120.

[111]
Chen P, Tang Z Y, Zeng Z M, Hu X F, Xiao L P, Liu Y, Qian X D, Deng C Y, Huang R Y, Zhang J Z, Bi Y L, Lin R K, Zhou Y, Liao H g, Zhou D, Wang C, Lin W B. Matter, 2020, 2 (6): 1651.

[112]
Chawla N V, Bowyer K W, Hall L O, Kegelmeyer W P. J Artif Intell Res, 2002, 16: 321.

[113]
Nandy A, Terrones G, Arunachalam N, Duan C, Kastner D W, Kulik H J. Sci. Data, 2022, 9 (1): 1.

[114]
Nandy A, Duan C, Kulik H J. J. Am. Chem. Soc., 2021, 143 (42): 17535.

[115]
Batra R, Chen C, Evans T G, Walton K S, Ramprasad R. Nat. Mach. Intell., 2020, 2 (11): 704.

[116]
Zanca F, Glasby L T, Chong S, Chen S, Kim J, Fairen-Jimenez D, Monserrat B, Moghadam P Z. J. Mater. Chem. C, 2021, 9: 13584.

[117]
Raza A, Sturluson A, Simon C M, Fern X. J. Phys. Chem. C, 2020, 124 (35): 19070.

[118]
Korolev V V, Mitrofanov A, Marchenko E I, Eremin N N, Tkachenko V, Kalmykov S N. Chem. Mater., 2020, 32 (18): 7822.

[119]
Kancharlapalli S, Gopalan A, Haranczyk M, Snurr R Q. J. Chem. Theory Comput., 2021, 17 (5): 3052.

[120]
Datar A, Chung Y G, Lin L-C. J. Phys. Chem. Lett, 2020, 11 (14): 5412.

[121]
Syah R, Al-Khowarizmi A, Elveny M, Khan A. Environ. Technol. Innov., 2021, 23: 101805.

[122]
Jablonka K M, Ongari D, Moosavi S M, Smit B. J. Am. Chem. Soc., 2020, 120 (16): 8066.

Options
文章导航

/

〈 〉