编者按:
CiteOpinion平台是中国科学院文献情报中心语义技术与知识挖掘实验室开发的代表作学术贡献引用评价循证分析工具,提供代表作学术贡献同行评价证据、科技论文引用句抽取、代表作引用句内容分析、代表作学术贡献评价循证分析报告等服务。该文基于2016–2020中国热点论文榜,选取数学领域的一篇高被引研究论文,利用CiteOpinion从引文内容的角度分析论文的科学贡献和实际影响,以期深入揭示热点论文被引用数据背后的信息。
该文由中国科学院文献情报中心CiteOpinion研究团队,知识系统部、智能情报重点实验室联合供稿*。
1 背景介绍
LWLT(2018)一文主要解决了当无法直接获取到样本均值和标准差时,如何在荟萃分析中利用所报告的中位数、最大最小值以及四分位数等来估算均值的问题。作者提出了根据样本大小设置平滑变化的权重来优化均值估算的方法。文章不仅提供了估算方程及其证明过程还提供了在线计算器(Excel电子表格)及经验权重系数方便直接计算。
LWLT(2018)一文一经发表便颇受关注,根据WoS数据库统计,2018年发表当年,被引频次达到14次,截至2021年9月14日,累计被引频次达到415次。LWLT(2018)一文入选数学领域ESI高被引论文,根据2021年InCites TOP1%高被引阈值,2018年发表的论文其被引频次需达到33次,LWLT(2018)一文的引用次数远高于这一阈值。
科技文献对学术界的主要贡献可以通过学术共同体对其引用及具体描述信息揭示。不过,单独使用被引频次指标很难全面深入展现论文的科学贡献和实际影响。另外,需要指出的是,在数学领域引用次数通常不被认可作为影响力的证据,尤其是纯数学领域,引用与研究问题的难度、后续研究的跟进和突破有关,数学领域被引频次偏低甚至零被引的论文也可能是高水平成果。基于此,分析数学领域论文的引用实质内容,对了解特定成果被传播、认可和使用的情况,对数学领域专家进一步判断该成果的学术价值和贡献则显得尤为重要。本文拟借助引用内容分析方法,更加深入具体地说明LWLT(2018)一文的创新性以及影响的广度和深度。通过追踪同行引用,本文试图回答以下问题。
(1)根据引用内容,是否可以初步发现LWLT(2018)一文的创新性及学术价值所在?
(2)根据引用内容,是否可以获得LWLT(2018)一文的研究对学术界产生影响力的证据,包括对本学科及其他学科的影响?影响范围及主要影响机构?
2 方法和数据说明
本文主要利用中国科学院文献情报中心研发的代表作学术贡献评价循证分析工具[2],采取人机协作方式,实现引用句自动抽取、学术贡献点分析及引用评价分析。
数据处理流程如图1所示。
图1
从WoS平台共获取LWLT(2018)一文的施引文献元数据415条(检索时间为2021年9月14日),通过CiteOpinion平台人机协作方式,总共成功解析施引文献307篇,获取引用句386条,其中他引文献304篇,引用句369条,自引文献3篇,引用句17条。成功获取引用内容的文献占施引文献总量的73.98%,篇均引用句约1.26条。
3 LWLT(2018)一文引用句概况
为了解LWLT(2018) 一文引用句概貌,下面对引用句词频、引用情感和引用句分类展开细粒度分析,该部分为保证分析的客观性,不包括自引引用句。
3.1 LWLT(2018)一文引用句词频分布
表1 LWLT(2018)一文引用句使用的词/术语(词频前20位)
| 位次 | 词/术语 | 词/术语性质 | 出现频次/次 |
|---|---|---|---|
| 1 | mean* | 数理统计专业术语,用于理解论文贡献的核心概念 | 186 |
| 2 | standard deviation | 数理统计专业术语 | 158 |
| 3 | luo et al* | 人名,论文第一作者 | 151 |
| 4 | median | 数理统计专业术语 | 127 |
| 5 | interquartile range | 数理统计专业术语 | 111 |
| 6 | study | 通用词汇 | 108 |
| 7 | wan et al* | 人名,论文合作者之一或其他论文作者 | 83 |
| 8 | range | 通用词汇 | 74 |
| 9 | data | 通用词汇 | 72 |
| 10 | iqr | 疑似interquartile range一词缩略语 | 50 |
| 11 | formula* | 与estimator等价的概念,用于理解论文贡献的核心概念 | 41 |
| 12 | value | 通用词汇 | 28 |
| 12 | sample size | 数理统计专业术语 | 27 |
| 14 | hozo et al | 人名,其他论文作者 | 20 |
| 14 | meta analysis | 论文结果的应用目的/场所 | 20 |
| 16 | estimator* | 用于理解论文贡献的核心概念 | 19 |
| 17 | continuous variable | 通用词汇 | 17 |
| 18 | continuous data | 通用词汇 | 15 |
| 19 | sample | 通用词汇 | 14 |
| 20 | patient | 通用词汇 | 13 |
| 20 | quartile | 数理统计专业术语 | 13 |
注:*表示该词做了人工规范。例如“formula”一词包含该词所有单复数形式、同义词、近义词以及加限定的短语等,“algorithm”,“equation”作为同义词或近义词被规范为“formula”。
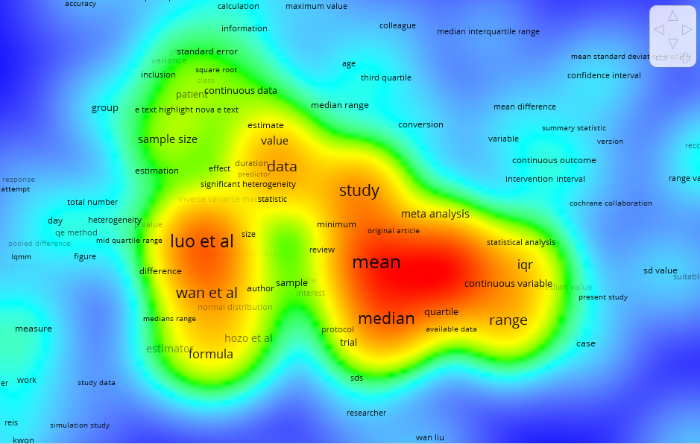
图2
图2
LWLT(2018)一文引用句词频分布图(局部)
注:绘图工具VOSviewer, coocurrence≥2,item数量为183,对部分词汇做了规范。
3.2 LWLT(2018)一文引用情感分析
除了一些已经取得国际声望的获奖论文,对大部分科技论文而言,引用情感表达是含蓄、克制的,但引用情感分析对判断论文价值有一定的参考辅助作用,同时对整理、提取能反映论文研究贡献的关键性引用句很有帮助。引用情感通常分为正向、中性和负向,正向引用句通常表达了施引文献作者对所引用的研究成果的强烈的肯定态度,或者将所引用论文与其他论文对比时认为效果更佳。表2给出了LWLT(2018)一文引用情感表达分布,可以看出,绝大部分引用为中性引用。图3给出了LWLT(2018)一文正向引用情感词云图,可以看出,这些表达肯定了LWLT(2018)一文的贡献,强调提供的计算结果更为准确,提供的方法是最新的优化估算方法、(计算工具)更具有鲁棒性、性能更为优越、有效等。中性的表达可能涉及一般性提及或实际应用等。而负向表达则有利于发现文章目前存在的局限或问题。
图3
3.3 LWLT(2018)一文引用句分类
CiteOpinion平台结合了引用情感、引用意图等判断对引用句进行分类,为被引文献的创新性评估和寻找影响力证据奠定基础。
结合CiteOpinion的机器分类结果,经人工检验判读之后,表3将LWLT(2018)一文的引用句分为4个类别,分别是创新性、应用性、先进性和其他。在369条引用句中,“创新性”引用句共12条,明确表达了LWLT(2018)一文所研究的计算方法是新颖的、有效的和得到验证的;“应用性”引用句共306条,直接或间接说明使用了LWLT(2018)提出的方法或工具来解决均值估算问题。“创新”和“应用”两类引用句互有交叉。“先进性”引用句共5条,高度集中在1篇施引文献,对比了LWLT(2018)一文相比其他论文揭示的计算方法更为优越。前3类引用句对于识别LWLT(2018)一文的学术贡献和学术影响均有价值。
表3 LWLT(2018)一文引用句类别分布
| 引用句类别 | 含义 | 引用句数量/条 | 所占比例 |
|---|---|---|---|
| 创新性 | 表示所研究的均值计算方法是新的、有效的和得到验证的 | 12 | 3.42% |
| 应用性 | 所提出的均值计算方法/工具得到应用 | 306 | 82.93% |
| 先进性 | 为解决均值计算问题,所提出的计算方法与其他人提出的方法相比较更为优越 | 5 | 1.36% |
| 其他 | 提及,仅为一般性事实陈述或用于比较但未揭示对比结果的好坏,有些引用内容无法直接判定与LWLT(2018)一文的关联性 | 55 | 14.91% |
其他类引用句共55条,是指未能很好归类的引用句,通常包括一般性事实陈述或者在比较中提及,但未揭示对比结果。其他类中还有些引用内容无法直接判定与LWLT(2018)一文的关联,通常是因为上下文信息不够充分、可能存在原始引用错误或者引用数据抽取问题,需要对施引文献进行全文阅读后方可判断。由于该类引用句占比较低,在实际分析中可忽略这部分数据。
4 讨论:LWLT(2018)一文的创新性与学术影响分析
依据第3部分的引用句分类识别结果,结合LWLT(2018)一文的摘要信息等,可进一步理解LWLT(2018)一文的创新性与学术影响。
4.1 LWLT(2018)一文的创新性和学术价值分析
LWLT(2018)一文的学术创新性和学术价值可以从作者自述或者他人引用两个角度来理解。
首先,根据LWLT(2018)一文的摘要,可以了解该研究提出了一个估算器(estimator),解决了样本均值(mean)的优化估算(optimal estimation)问题。作者针对之前研究均值计算时忽略样本大小(sample size)的问题,提出可以采用在样本量中嵌入平稳变化权重(smoothly changing weight)的方式来实现更优化的估算。作者还提供了开发的估算器,即在线Excel电子表格,以方便用户简化计算样本均值过程。
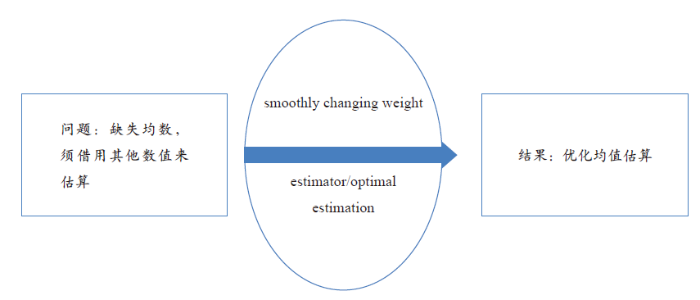
在上述表述中,可提炼的主要概念包括estimator/optimal estimation, smoothly changing weight, mean,其中均值问题(即mean一词)为研究对象,而estimator/optimal estimation和smoothly changing weight则代表了作者提出了问题的新的解决思路和方法。基本理解框架如图4。
图4
其次,对照引用句词频分析结果,可以看出均数(mean)、公式/算法(formula)、估算器(estimator)等词出现在引用句前20高频词中,与文摘中的论文核心概念吻合度较高。
表4 表征LWLT(2018)一文创新性贡献的关键性引用句
| 引用句 | 第一作者/通信作者 | 来源(出版年) |
|---|---|---|
| The methods developed by Luo et al. 17 and Wan et al. 15 are the best-performing formula-based methods for estimating the sample mean and standard deviation respectively. | McGrath, Sean/Benedetti, Andrea | Statistical Methods in Medical Research(2020) |
| We also consider the methods more recently developed by Luo et al. (2016). Under the assumption that the outcome variable is normally distributed, the methods of Luo et al. (2016) optimize the sample mean estimators recommended by Wan et al. (2014). | McGrath, Sean/Benedetti, Andrea | Biometrical Journal (2020) |
| The method given by the Tiejun Tong group was used to calculate the closest approximation of mean and standard deviation (SD) from median and interquartile range (IQR) 22,23. | Tsiapakidou, Sofia/Mikos Themistoklis | International Urogynecology Journal(2021) |
| Therefore, the proposed equation appears to be capable of providing a more accurate estimation of the sample mean regardless of the distribution.18 | Sin, Jeremy Cheuk Kin/ Sin, Jeremy Cheuk Kin | Journal of Intensive Care Medicine(2021) |
| Studies lacking important pertinent information, eg, mean and standard deviation of NFRthr in FM patients and/or in healthy controls, were handled as follows: i) If the median and range (interquartile range or first-quartile and third quartile) were mentioned: we used an update and robust methodology to calculate the required statistics; 32…… | Amiri, Mohammadreza/Kumbhare, Dinesh | Journal of Pain Research(2021) |
2 注:此处Luo2016年发表的文章系LWLT(2018)一文正式发表前在arxiv.org发表的同名论文。
4.2 LWLT(2018)一文的学术影响分析
LWLT(2018)一文的学术影响可以从三个角度理解,一是哪些研究是在LWLT(2018)一文基础上的进一步拓展?二是有哪些国家/地区和机构的学者借助LWLT(2018)一文提供的估算方法和工具开展相关统计和荟萃分析?另外,还可以通过与LWLT(2018)一文共被引情况,了解哪些研究与LWLT(2018)一文产生了共同的学术影响。
4.2.1 对扩展研究的影响:对均值算法的改进
除LWLT(2018)一文的作者外,目前只有2篇数理统计领域的论文引用了LWLT(2018)一文,两篇论文的作者均为来自加拿大麦吉尔大学的McGrath, Sean等人。
在2020年初发表的“Meta-analysis of the difference of medians”一文中,McGrath等人主要对比了基于中位数和基于转换两种竞争性统计方法的性能。该文对LWLT(2018)一文引用高达16次,说明二者所讨论内容高度相关。文章肯定了LWLT(2018)一文所提出的样本均值估算器方法优于之前发表的研究,详细引用内容如下:
我们还考虑了Luo等人(2016)2最近开发的方法。在结果变量为正态分布的假设下,Luo等人(2016)的方法优化了Wan等人(2014)推荐的样本均值估计器。(原文参见表4)
2020年,McGrath等人发表了“Estimating the sample mean and standard deviation from commonly reported quantiles in meta-analysis”一文,声明当样本非正态分布时,解决了更准确地估算样本均值和标准差的问题。该文对LWLT(2018)一文的引用次数为12次。从引用句中可以看出Sean对LWLT(2018)一文的批判性接受,McGrath首先肯定了LWLT(2018)一文的贡献(见表4),在随后的引用中提到:
Luo等人的样本均值估计器17和Wan等人的样本标准差估计器15是基于公式的方法,是在假设结果变量为正态分布的情况下得出的。
(原文:The sample mean estimator of Luo et al.17 and the sample standard deviation estimator of Wan et al. 15 are formula-based methods that are derived from the assumption that the outcome variable is normally distributed.)
从上述分析可以看出,LWLT(2018)一文的学术贡献得到领域同行的认可和发展,总体看来,童铁军团队在推动统计分析中均值估算等问题研究方面表现更为活跃。
4.2.2 对主要应用领域的影响:在荟萃分析中的具体应用
为了解LWLT(2018)一文对荟萃分析的影响,本文在数学领域之外,选取了其他学科对该文的应用性引用句开展分析。在应用性引用句中共获取到302篇施引文献和339条引用句,下面具体分析LWLT(2018)一文影响到的学科领域及作者情况。
(1)LWLT(2018)一文所影响的学科领域
从表5可以看出,LWLT(2018)一文影响到的主要学科领域是医学领域,在环境科学和生态学的荟萃分析中也有少量应用。
(2)LWLT(2018)一文所影响的作者国别和所在机构分布
图5
表6 引用LWLT(2018)一文排名前10的机构
| 排名 | 机构名称(国家/地区) | 论文数量/篇 |
|---|---|---|
| 1 | 四川大学(中国) | 15 |
| 2 | 中国医学科学院北京协和医学院(中国) | 12 |
| 3 | 浙江大学(中国) | 11 |
| 4 | 哈佛大学(美国) | 8 |
| 4 | 胡安-卡洛斯国王大学(西班牙) | 8 |
| 4 | 多伦多大学(加拿大) | 8 |
| 7 | 马德里大学(印度) | 7 |
| 7 | 哈佛大学医学院(美国) | 7 |
| 7 | 圣卡洛斯医院(西班牙) | 7 |
| 7 | 华中科技大学(中国) | 7 |
4.2.3 共同分享影响的研究:与LWLT(2018)一文同时被提及的研究
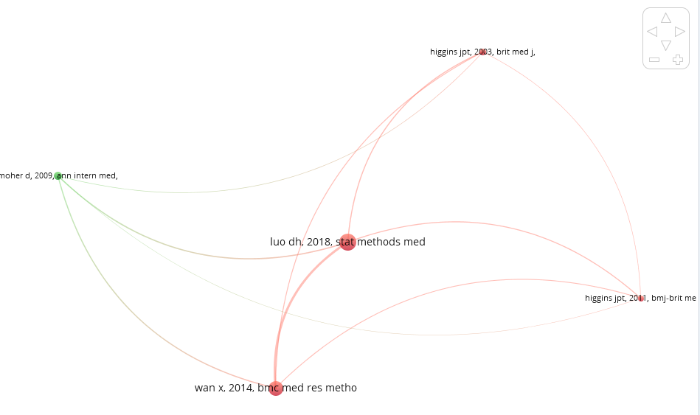
在LWLT(2018)一文的引用句中,发现在提及LWLT(2018)一文的时候,同时也提及其他作者的成果,这些成果共同为解决荟萃分析统计问题提供了帮助。通过WoS获取了LWLT(2018)一文304篇施引文献的参考文献,通过共被引分析发现以下4篇文献与LWLT(2018)一文具有高度相关性(图6)。LWLT(2018)一文的合作者之一万翔在2014年发表的论文[11]与LWLT(2018)最为相关,该文解决了优化样本标准差估算的问题。Moher等人在2009发表的PRISMA声明[13]是关于系统回顾和荟萃分析报告质量控制的一个声明。Higgins等人在2011年和2003发表了有关随机试验中偏倚风险问题的研究[13,14]。总体来看,这些共被引文献共同支撑了开展荟萃分析应采取的正确数据处理方式。
图6
5 小结
根据上述分析可知,LWLT(2018)一文得到同领域学者认可并在医学荟萃分析中产生了重要影响。可以归纳如下。
(1)LWLT(2018)一文解决了荟萃分析中无法直接获取均值时,可通过提供的中位数、四分位数等其他数值来解决均值估算问题。作者在提供计算公式及其证明的同时,还提供了在线工具,方便读者直接使用。
(2) LWLT(2018)一文的突出贡献体现在应用性上,该文应用性引用句占比达82.93%。
(3)LWLT(2018)一文得到同领域学者认可,认为在假设结果变量为正态分布的情况下,优化了之前学者提供的样本均值估计器。
(4)在数理统计领域,对LWLT(2018)研究有后续发展的团队主要是童铁军团队自身和来自加拿大的McGrath等人。LWLT(2018)一文的作者们对相关问题的研究处于活跃和领先状态,这与团队在解决估算算法的同时,非常注重分析工具开发密不可分,正如作者团队在文献[9]中提到的“我们注意到Walter和Yao也提供了一个估计样本标准差的数值解决方案,而分析公式(工具)的缺乏使其不太容易被使用者接受”。McGrath等人进一步推动了当数值非正态分布时,优化均值估算的问题。
(5)LWLT(2018)一文引起了医学荟萃领域学者的关注,占比98.68%的医学施引文献在荟萃分析中参考利用了该文提供的均值估算方法。对其他学科,如环境科学等领域荟萃分析的影响也逐步显现,但数量明显少于医学领域。由于该论文刊发在医学杂志,可能还没有引起更多非医学领域学者的关注。
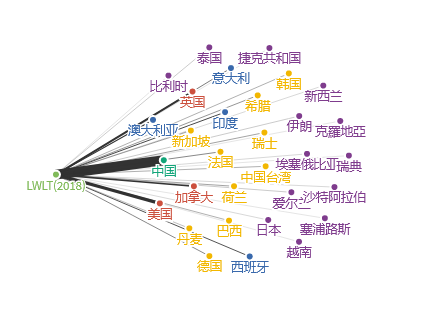
(6)LWLT(2018)一文在全球范围内获得相关学者的关注和引用,来自中国的引用最多,达到154篇次,其次是美国和英国,均为30篇次以上。
本文利用CiteOpinion循证分析工具较为快捷便利地获取到引用内容数据和初步分析结果,在结合人工判读的基础上,对LWLT(2018)一文的学术贡献和影响开展了初步分析。由于目前引用内容的获取仍受制于全文获取、引用文本解析和文本分类技术,在具体开展分析时也受限于分析者的学术背景,本文可能存在一定偏见。引用内容的解读,需要依据领域专家做出最终判断,本文的结果谨为专家解读提供参考。
参考文献
Optimally estimating the sample mean from the sample size, median, mid-range, and/or mid-quartile range
[J].
CiteOpinion代表作学术贡献引用评价循证分析
[EB/OL][
Estimating the sample mean and standard deviation from commonly reported quantiles in meta-analysis
[J].
Meta-analysis of the difference of medians
[J].DOI:10.1002/bimj.201900036 URL [本文引用: 1]
The use of urinary biomarkers in the diagnosis of overactive bladder in female patients. A systematic review and meta-analysis
[J/OL].
Hypophosphatemia and outcomes in ICU: A systematic review and meta-analysis
[J].
Fibromyalgia and nociceptive flexion reflex (NFR) threshold: A systematic review, meta-analysis, and identification of a possible source of heterogeneity
[J].
Estimating the mean and variance from the five-number summary of a log-normal distribution
[J].DOI:10.4310/SII.2020.v13.n4.a9 URL [本文引用: 1]
Optimally estimating the sample standard deviation from the five-number summary
[J].DOI:10.1002/jrsm.1429 [本文引用: 2]
Estimating the reference interval from a fixed effects meta-analysis
[J].
Estimating the sample mean and standard deviation from the sample size, median, range and/or interquartile range
[J].
Preferred reporting items for systematic reviews and meta-analyses: The prisma statement
[J].
The cochrane collaboration’s tool for assessing risk of bias in randomised trials
[J].