近些年来,荟萃分析（meta-analysis）作为一种整合数据的统计方法越来越受到人们的关注,其优势在于能够综合多个针对同一问题的研究,克服单个研究样本量不足的问题,从而得到更可靠的结论。荟萃分析的起源可追溯至17世纪,这种整合研究的思想最先被应用于天文学研究中,并由以George Biddell Airy为代表的天文学家将此种统计方法总结成书,成为当时的经典教材。20世纪初,统计学家Karl Pearson第一次正式在《英国医学杂志》中运用整合分析多个研究的方法对于伤寒疫苗的有效性进行研究。此后,Ronald Fisher和William Cochran分别将荟萃分析的思想应用于农业及医学领域。之后的几十年,经过研究者的不懈努力,荟萃分析的方法不断发展。1976年,Gene Glass正式将此类方法命名为荟萃分析,并指出荟萃分析是对于多个分析研究的汇总分析（Educ. Res., 1976, 5, 3-8）。此后,荟萃分析持续发展并纳入Cochran 系统评价的指导手册中。

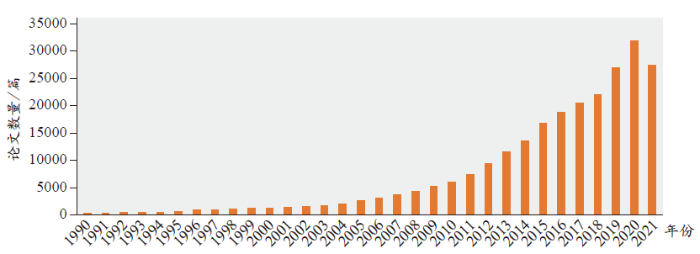
随着理论方法的完善加之应用简便等优势,荟萃分析越来越受到各学科的关注。目前,其广泛地应用于循证医学、教育学、经济学、天文学、环境科学、农业科学等多个学科中。Web of Science显示以荟萃分析为主题的文献发文量呈现明显的增长态势,如图1所示。其中以在循证医学中的应用最为常见,一个经典案例为1990年发表的对于七组随机对照试验的整合分析,研究结果显示对过早分娩妇女进行皮质类固醇治疗能够显著降低早产儿死亡率约30%至50%。而在此之前,从未有过类似的综合研究,导致大部分妇产科医生并没有认识到此种治疗方法的有效性,因此当时许多早产儿可能遭受了不必要的痛苦甚至死亡（BJOG-Int J Obstet GY, 1990, 97, 11-25）。

在循证医学中,研究者往往需要首先对于选定的研究问题进行系统性评价,包括文献获取、文献筛选、文献纳入,进而对最终纳入的研究进行荟萃分析。近些年来,随着文献数量的爆发式增长,数据的报告形式也呈现出多样性。例如,对于二分类变量,有些文献报告优势比（odds ratio）,而有些文献报告风险比（risk ratio）;对于连续型变量,有些文献报告样本均值和标准差以刻画数据的主要特征,而有些研究中数据呈现出一定的非正态性（如偏态性）,研究者会选择报告代表性分位数（如：中位数、最小最大值和/或四分之一以及四分之三分位点,合称为五数综合）。

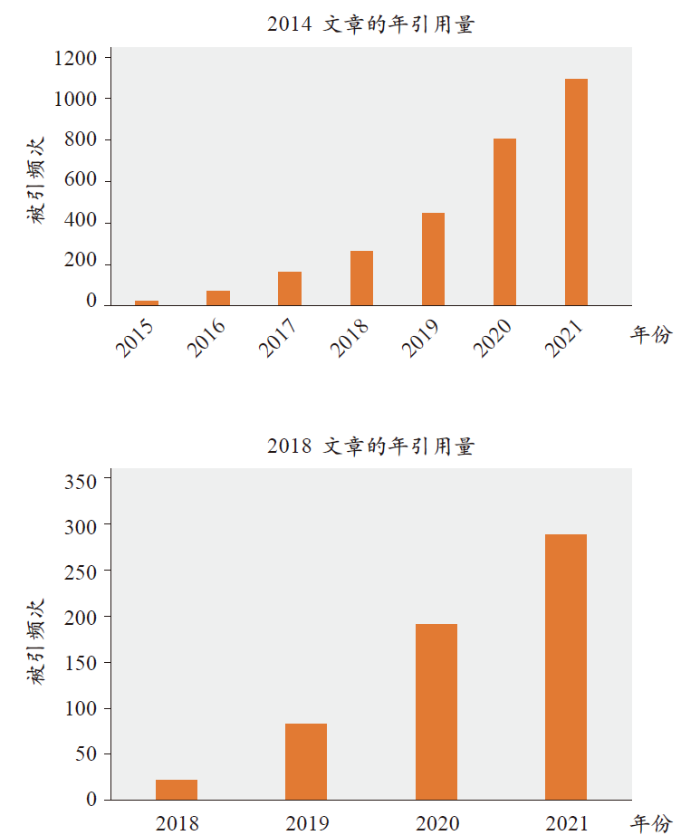
以连续型结果为例,荟萃分析可以直接对样本均值及标准差类型数据进行整合分析,而对于分位数数据,传统的荟萃分析无法直接整合。考虑到直接排除这些数据可能造成重要信息损失,因此在荟萃分析前进行数据转换,也即将报告的分位数转化为样本均值和标准差,便成了自然的需求。基于此种需求,多篇文献在数据正态分布的假设下,提出了数据转化的方法（如BMC Med. Res. Methodol., 2014, 14, 135;Stat. Methods. Med. Res., 2018, 27, 1785-1805;Res. Synth. Methods., 2020, 11, 641-654）。以我们在2018年的工作为例,其有效地利用了正态分布下样本分位数信息与均值参数的关系,给出无偏估计的同时,通过调整对不同分位数的权重得到更有效的估计。值得注意的是,这三篇文章在发表后迅速被大量引用,截至2021年10月28日,谷歌学术显示其分别被引用2 876,582及36次,前两篇文章的年引用增长模式如图2。此类文章颇受关注得益于荟萃分析中对此种方法的重要需求,同时文章中提出的数据转换方法准确、简明易懂,作者还提供了在线计算器以便研究者使用。(https://www.math.hkbu.edu.hk/~tongt/papers/median2mean.html)

尽管以上方法被研究者广泛认可并引用,但一个值得注意的问题是上述方法均基于数据正态性的假设,也即数据转化的准确度很大程度取决于数据是否真正来自正态总体。若数据并非来自正态总体（例如来自偏态总体）,那么此类方法转换得出的结果可能会产生偏差。于是一个自然的问题是：是否能够基于文献中报告的分位数及样本量信息判断数据的对称性或正态性,从而对后续数据转换方法的应用进行指导?从以往文献看,仅通过三五个分位数来进行假设检验似乎难度较大,在我们最新的工作中,一类偏态性检验的方法恰好针对此类问题给出了解决办法,该方法以数据正态性为原假设,以分位数的偏度度量值为检验统计量,能够有效地检验出数据相对于正态性的偏离,其中最大的亮点为其利用统计量在原假设下的确切分布而不是渐近分布,更好地利用了样本量的信息,从而极大地提升了有限样本下检验的统计功效。

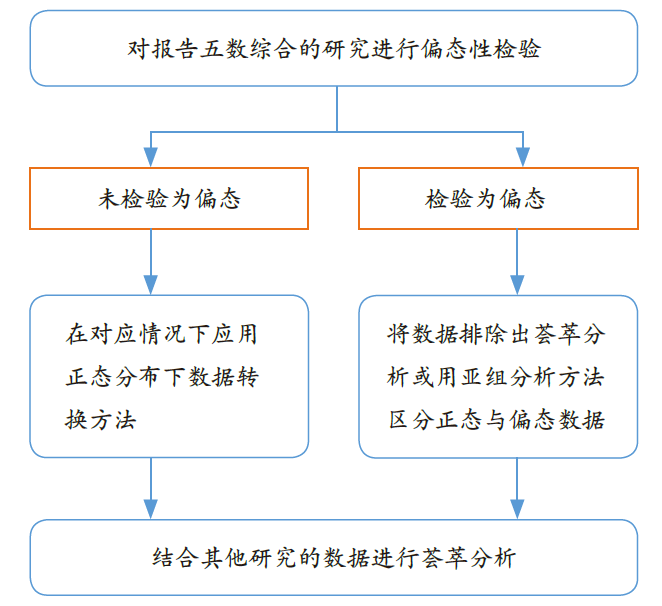
同时,我们也给出了一个在荟萃分析中处理报告分位数的研究框架,如图3所示。具体来讲,在对系统评价中报告五数综合的数据进行偏态性检验后,若数据未被检验为偏态,则可放心使用上述正态分布下的数据转换方法;而若数据被检验为偏态,我们推荐将此数据排除出后续荟萃分析,或是选择使用亚组分析将正态数据和偏态数据区分开,以保证最终得到的结果不会误导读者,甚至给出更多信息供读者参考。同时,以上对于五数综合数据进行荟萃分析的框架,包括偏态性检验以及数据转换的方法也被加入上述在线计算器,以便为研究者提供数据的更多信息,也使得数据转换更加准确,在线计算器的使用演示如下（以报告样本量、中位数和最小最大值的情形1为例）。

步骤1：找到报告的数据对应情形,将数据输入对应位置,并点击“Detect the skewness”进行偏态性检验;

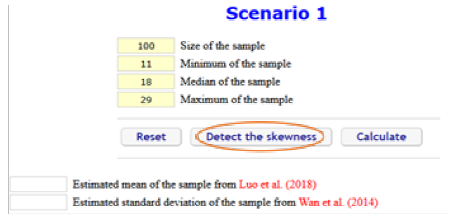
步骤2：对此未检验为偏态的数据,继续点击“Calculate”估计样本均值和标准差;

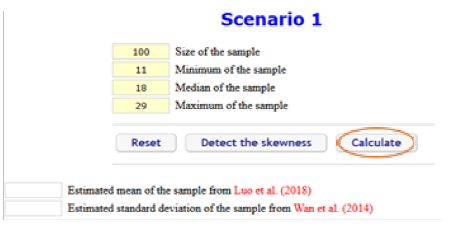
结果：得到样本均值和标准差的估计。

总而言之,我们新提出的对于五数综合数据的处理框架和在线计算器为应用者提供了详细的指导和便捷的计算工具,将在之后的荟萃分析及循证研究中起到重要作用。同时,纵观荟萃分析,此类工作只是整体框架下的冰山一角,其中还有大量有意义的问题亟待研究者解决,例如荟萃分析中模型的选择、异质性的刻画以及发表偏倚等问题。相信随着理论体系的不断完善及各种便捷应用软件的升级,会有更多经典的荟萃分析方法在循证研究中起到重要指导作用。