剪切应力和剪切变形速率之间不满足线性关系的流体称为非牛顿流体。生活中可见大量非牛顿流体, 如油脂、油漆、聚合体、胶体;生物体内的血液、淋巴液、细胞液、脑脊液等等。随着科学技术的发展,非牛顿流体力学在许多工业生产和科学领域的应用越来越多。非牛顿流体力学的研究对这些工业的发展具有重大现实意义。

非牛顿流体的物质构成和其所表现的行为特征远比牛顿流体复杂,传递过程中呈现一系列“奇特”、“反常”的物理现象。如管流剪切变稀现象、应力松弛、蠕变、滞后、残余应力、挤出物胀大、粘弹性回复、无管虹吸、湍流减阻及滑移现象。人们提出了众多形式的本构方程来表征非牛顿流体的各种复杂流动、热质输运行为。如 Ostwald de Waele 幂律流体、Binghan流体、Casson流体、Maxwell流体、Olroyd-B流体和Burgers流体模型等。

粘弹性流体是介于粘性流体和弹性固体之间,同时表现出粘性和弹性性质的一类特殊的时变性非牛顿流体。流体受外力作用而发生形变或流动,在不超过屈服强度的条件下,当剪应力除去以后,它的变形能随时间逐渐回复或者能部分的复原。粘弹性流体的粘度函数不仅与应变速率有关,还与剪切持续时间有关。

流体的粘弹性可分为线性粘弹性和非线性粘弹性。线性粘弹性即应力、应变和应变速率之间成线性关系。粘弹性流体往往只能在较小的形变或形变速率下才出现线性粘弹性特性。在较大的应变或剪切速率下,应力、应变和应变速率之间一般不成线性关系,即流体呈现非线性粘弹性。对非线性粘弹性状态下的流体,所测的流变性数据受实验参数和测量系统几何尺寸的影响非常大。目前人们对粘弹性流体流变性的认识及研究在很大程度上仍停留在线性粘弹性范围。

在经典的传热或传质问题的研究中,最基本的也是最成功的描述传热或传质问题的本构关系模型是Fourier定律或Fick定律。但是,人们发现这两个定律存在自身的局限性。以Fick 定律为例,由描述一维扩散现象的Fick定律本构方程可以得到控制方程：$\frac{\partial P}{\partial t}=D\frac{\partial^{2}P}{\partial x^{2}}$,对于初始条件$P(x,0)=\delta(x)$,可得到方程的高斯形式的解：

从解的表达式中可以看出,任何微小的扰动在很短的时刻、无穷远的位置都会有有限数量的粒子,这是与物理相违背的。

Cattaneo通过引入松弛时间系数克服了Fick定律的不足,提出修正的本构模型如下：

其传播速度为：$v=(D/ \xi)^{1/2}$, $\xi $是一个非负的常数,指的是扩散松弛时间。取极限$\xi →0$,方程 (1.2) 即退化到经典的Fick定律。

通过引进松弛参数,扩散方程从抛物型变成双曲型。类似,人们将Cattaneo通量模型应用到传热问题的研究。Cattaneo模型仅包括时间偏导数,不适用于流动的介质。Christov推广了Cattaneo模型,把时间导数修正为上随体导数,成功保存了材料不变性构想。近几年,Cattaneo-Christov模型的研究吸引了很多学者的关注。Straughan^[1]利用该模型研究重力作用下的不可压缩牛顿流体的水平层热对流问题。Haddad^[2]利用该热张量模型研究了Brinkman多孔介质的热不稳定性。考虑到粘弹性流体松弛特性,本文作者基于流变协同机制^[3,4]将Cattaneo-Christov热张量模型引入到Maxwell粘弹性流体在拉伸板上耦合流动和传热问题,同时考虑了速度滑移边界。利用同伦解析的方法求得解析解,分析了各个相关参数对速度和温度场的影响,并与经典Fourier定律热通量模型进行了比较。

粘弹性流体同时具有粘性和弹性特征。用弹簧表示弹性,阻尼器表示粘性,将两者以一定的方式结合成一个力学系统,这个系统同时反映流体具有的粘性和弹性特征。典型的粘弹性流动模型有：Maxwell模型,Kelvin-Voigt模型,Jeffreys模型和Burgers模型。这些力学模型由离散的弹性元件与粘性元件,即弹簧和阻尼器以不同方式组合而成。

弹簧变形为$\gamma_{1}$,阻尼器变形为$\gamma_{2}$,根据胡克定律为

按照牛顿内摩擦定律有

式中$\tau$为应力,G、$\mu$分别为剪切弹性模量和粘性系数,均为常数,$k_{2}=\dot{\gamma}_{2}$（“·”表示对时间微分）。

Maxwell模型等效于一个弹簧与一个阻尼器的串联,能准确描述应力松弛现象。设总伸长为 $\gamma $,则有

或者

此即Maxwell粘弹性流体的本构方程。Kelvin-Voigt 模型等效于一个弹簧与一个阻尼器的并联,能准确描述蠕变现象,即应变恢复现象。对于Kelvin-Voigt模型,受力为

即总应力是弹簧所受力与阻尼器所受力之和。应用胡克定律和牛顿内摩擦定律可导出微分型本构方程：

Jeffreys模型描述的是一个弹簧与一个阻尼器并联后,再与一个阻尼器串联所构成的物理模型。Jeffregs模型的本构方程为：

上式中$\lambda_{1}$,$\lambda_{2}$,$\mu_{0}$均为物质参数。

Burgers模型的本构方程为：

上式中的p₁,p₂,q₁,q₂均为物质参数。Kelvin-Voigt模型中由于阻尼器的变形受到弹簧的约束,因此,该模型一般不适合用来表示液体的流动。Maxwell模型和Jeffreys模型原则上可用于描述粘弹性液体的流动。不过,这两个模型都是线性模型。如果将Maxwell模型和Jeffreys模型中的时间导数修正为随体导数,则可演化出相应的非线性模型。

Maxwell流体模型是研究粘弹性流体特性的重要模型之一,其本构方程为：

其中T表示柯西应力张量,-p表示流体静压力,I表示单位张量, A₁=L+L^T表示第一Rivlin-Ericksen张量, L表示速度梯度, $L^{T}$表示速度梯度张量的转置,$\mu$表示Maxwell流体的动力粘度, $\lambda_{1}$表示松弛时间。

考虑到Maxwell流体在一无限平板上的二维稳态边界层流动,假设流体是静止的,平板沿x轴方向运动,

则描述质量和动量守恒的控制方程为：

对于上述的控制方程,本文考虑具有滑移特性的边界条件

其中a是正常数, u、v分别表示流体沿x、 y方向的速度分量,表示分子的平均自由程,$\sigma_{v}$表示切向动量协调系数。

考虑到Maxwell流体的松弛特性,基于流变协同原理,我们引入具有松弛特征的Cattaneo-Christov热通量模型,其温度场本构方程如下：

在此热通量模型中,q表示热通量, $\lambda_{2}$为热通量松弛时间参数, T表示流体的温度, k表示流体的导热系数,v=(u,v)是Maxwell流体的速度矢量。当$\lambda_{2}=0$, 方程(3.6)退化为傅立叶热传导定律。由于考虑流体是不可压缩的, 满足条件$\bigtriangledown · V=0$, 方程(3.6) 可以化为下面的形式

描述流体稳态层流边界层能量守恒方程如下：

将方程(3.7) 和(3.8) 联立消去热通量q,便得到下面的温度场边界层控制方程：

其中$\alpha=k/\rho c_{p}$表示流体的热扩散系数,c_p是流体的比热。

上述温度场方程的边界条件为：

当y=0时,T=T_W;当$y→\infty$时,$T→\infty$(3.10)

注意到由动量方程和能量方程联立的边界层方程组中,方程 (3.3) 和 (3.9)都呈现强非线性,为避免直接求解的困难,引入下面无量纲变换：

其中是流量函数,满足 。方程（3.3）和（3.9）变换为：

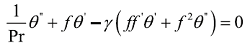
其中 是普朗特数。

边界条件（3.4）~（3.5）和 （3.10）化为如下形式：

其中

下面运用同伦分析法求解相似解方程组（3.12）~（3.15）。

首先,初始猜测解满足边界条件（3.14）和（3.15）,可以选择为：

为便于求解,选取如下辅助线性算子：

非线性算子的形式为：

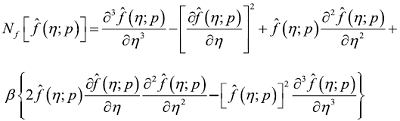
在式（3.17）中的辅助线性算子有如下形式的通解：

其中C₁,C₂,C₃,C₄和C₅是任意常数。

构造如下的零阶形变问题

相应的边界条件为：

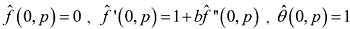
其中$p\in [0,1]$是为了构造同伦而设置的嵌入参数,$h_{f}$和$h_{\theta}$是非零辅助参数。对于方程（3.21）和（3.22）,它们的解的特殊情况为：当p=0时 , ,当p=1时, 。因此,将 和 关于参数p展开为如下的泰勒级数形式：

其中 , .

通过选取合适的$h_{f}$和$h_{\theta}$使 和 在p=1处收敛。所求的解可表示为如下形式：

为了得到$f_{m}(\eta) $和$\theta_{m}(\eta) $,(m=1,2,3,…),考虑下面的高阶形变方程：

其中

对应于方程 (3.27) 的边界条件：

通过求解满足边界条件（3.31）的高阶形变方程（3.27）,依次可以得到$f_{m}(\eta) $和$\theta_{m}(\eta) $,(m=1,2,3,…),然后将它们代入式子（3.26）,便可得到所求问题(3.12)~(3.15)的近似解析解。利用Matlab数学计算软件,计算到$f_{8}(\eta) $和$\theta_{8}(\eta) $,即得到了方程（3.12）~（3.15）的8阶同伦近似解析解。

非零辅助参数$h_{f}$和$h_{\theta}$强烈影响着同伦分析解的收敛性。因此我们必须选取合适的$h_{f}$和$h_{\theta}$,以确保求出的同伦解是收敛的。做出图3-1来找出求得的8阶同伦近似解的收敛区域。从图3-1(a)中可以知道速度场的同伦解的收敛区域是$-0.9≤h_{f}≤-0.1$。图3-1(b)显示流体温度场的同伦近似解的收敛区域是$-1.2≤h_{\theta}≤-0.4$。因此,可以选取$h_{f}=h_{\theta}=-0.6$,此时速度和温度场的同伦解都是收敛的。图3-2显示了流体速度$f'(\eta)$和温度$\theta(\eta)$的8阶同伦近似解与用有限差分法得到的数值解的吻合程度。从图3-2中,可以看出所得到的同伦解几乎与数值解一致。

利用同伦分析方法和Matlab数学软件求解相似解方程组（3.12）~（3.15）可以得到Maxwell流体边界层流动及传热问题的近似解析解。下面通过特定参数情况的计算结果图像,分析讨论各相应参数对流体速度场和温度场的影响。

上随体Maxwell模型有一个弹性项,被用来反映粘弹性流体的弹性性质。在粘弹性流体流动时,弹性力对其流动和传热有一定程度的影响。图3-3到图3-5分别显示了弹性参数$\beta$对Maxwell流体速度和温度分布的影响。当弹性参数$\beta=0$时,不考虑或者忽略了弹性力的影响,流体模型变为牛顿流体模型,当弹性参数的值逐渐增大时,弹性力对流体流动会有更大的影响。图3-3和图3-4分别显示$f(\eta)$和$f'(\eta)$随着的增加而变小,这说明速度边界层随着 的增加变得越来越薄。图3-5显示流体温度$\theta(\eta)$随着$\beta$的增加而升高,这反映出弹性力促进了粘弹性流体的传热效率。图3-6和图3-7描述了速度滑移系数分别对$f(\eta)$和$f'(\eta)$的影响,从图中可以看到当增加滑移系数 b的值时,速度分布$f(\eta)$和$f'(\eta)$的值会变小,表明滑移系数的增加会使流体速度边界层变薄。

图3-8描述了参数$\gamma$对流体温度$\theta(\eta)$的影响,当$\gamma = 0$时,流体温度变为运用傅立叶定律时的情形。从图可以看出,流体的温度随着$\gamma$的增加而降低,这说明$\gamma$的增加会阻碍流体温度边界层的发展。图3-9显示普朗特数Pr对温度的影响,随着普朗特数Pr的增大,温度边界层变得越来越薄。

非牛顿流体在日常生活和科学技术等许多领域都有着非常重要的应用。近几十年来人们在非牛顿流体流变特性研究方面已经取得了重大进展,但是对于其传热传质机理仍然没有得到很好理解,一直照搬牛顿流体导热来处理。作者提出非牛顿流体传热、传质问题遵循流变协同机制,即应该基于流体的流变特性来构建其热质输运本构关系模型。本文以上随体导数Maxwell粘弹性非牛顿流体模型为例,阐述了如何根据该类流体的松弛特性,引入Cattaneo-Christov热通量公式,提出Maxwell粘弹性流体流变协同的传热本构方程模型,引入适当的相似变换和同伦分析法得到了模型的近似解析解,并详细分析讨论了一些参数变量对非牛顿流体速度场、温度场及剪切力场的影响。在新热通量模型中,傅立叶定律只是一种特殊情况。本文研究中还考虑了边界滑移的影响,并且详细讨论了这些实际因素对流体速度场和温度场的影响。

非牛顿流体种类繁多,特性复杂,尚有许多问题需要更加深入的研究才能解决,也恳请各位专家学者能给予不吝赐教。