日常生活中信号无处不在,如光信号、电信号、声音信号、手机信号、雷达信号等等。在数学上,模拟信号(analog signal)是定义在时间或空间上的实(或复)值连续函数。人们经常需要对信号进行各种处理,以方便信号存储、传输和分析。首先,需要通过感知器对信号进行测量或检测,以数值的形式捕获信号,即数字信号。这一过程称为采样,通过测量模拟信号在一系列时间点或空间位置上的函数值来实现。对采样数据进行插值处理,以试图还原原始模拟信号。上述采样与插值重构的过程是否可以精确地恢复原信号,或者能够以何种精度近似地恢复原信号?为了回答这一问题,首先需要限定信号的范围,即所关注的是哪一类信号模型。若信号模型涵盖的范围过于广泛,在理论上将难以实现插值重构原信号。传统的信号处理理论对这一问题给出了近乎完美的回答。粗略地说,根据奈奎斯特-香农(Nyquist-Shanno) 采样定理,若信号具有有限带宽,并且采样频率不低于带宽的两倍,那么原信号即可从采样数据中得到完全复原,并且重构过程可由著名的Shanno-Whittaker插值公式给出。这里有限带宽即为信号模型。
日常生活中信号无处不在,如光信号、电信号、声音信号、手机信号、雷达信号等等。在数学上,模拟信号(analog signal)是定义在时间或空间上的实(或复)值连续函数。人们经常需要对信号进行各种处理,以方便信号存储、传输和分析。首先,需要通过感知器对信号进行测量或检测,以数值的形式捕获信号,即数字信号。这一过程称为采样,通过测量模拟信号在一系列时间点或空间位置上的函数值来实现。对采样数据进行插值处理,以试图还原原始模拟信号。上述采样与插值重构的过程是否可以精确地恢复原信号,或者能够以何种精度近似地恢复原信号?为了回答这一问题,首先需要限定信号的范围,即所关注的是哪一类信号模型。若信号模型涵盖的范围过于广泛,在理论上将难以实现插值重构原信号。传统的信号处理理论对这一问题给出了近乎完美的回答。粗略地说,根据奈奎斯特-香农(Nyquist-Shanno) 采样定理,若信号具有有限带宽,并且采样频率不低于带宽的两倍,那么原信号即可从采样数据中得到完全复原,并且重构过程可由著名的Shanno-Whittaker插值公式给出。这里有限带宽即为信号模型。
为了方便,我们仅局限于离散的数字信号。基于有限带宽假设的信号编码包括采样、变换和压缩编码3个步骤。首先,通过采样来获取数字信号x,即n维实向量。根据奈奎斯特-香农采样定理,采样频率不得低于带宽的两倍。对于带宽非常高的信号,高频采样导致数字信号x的长度n非常大。其次,选取适当的正交变换Ψ,如离散余弦变换,并计算变换系数s=ΨT x。通常s是可压缩的,即s的n个分量按绝对值从大到小快速衰减。最后,选取s的p(通常p远远小于n)个绝对值较大的分量,对该p个分量所对应的位置进行编码,并舍弃其余的n–p个分量。这就是常说的有损压缩(lossy compression),压缩后数据量大大减少,存储与传输信号的效率更高。以上是传统信号处理中变换编码的大致过程,即采样、变换、压缩编码。通常对静态图像的压缩比例大约为10:1到20:1。图1给出了运用层数为2的Haar小波变换对大小为512乘512的Lena图像以比例10:1进行压缩的例子。显然,人类的肉眼很难分辨出压缩前后的图像。压缩编码技术正是利用了人类视觉系统的这一固有缺陷。
然而,变换编码技术有几个明显的缺陷。第一,对于高频信号,维数n非常大,而压缩后的数据量p通常远远小于n,即感知器收集的大量数据在编码过程中将被遗弃,造成效率不高与资源浪费。第二,需要先计算s的所有分量,然后才能获知p个主要分量的位置。第三,需要对p个主要分量的位置进行编码。第四,不同的主要分量所承载的信息量是不同的。在数据传输过程中,若某些主要分量被丢失,将导致大量的信息缺失。是否可以设计一种直接获取压缩数据,即采样数据量为p,并且可以从压缩数据中重构原始信号的方法?这样一来,不但加快了采样过程,节约了采样成本,而且省去了变换编码的过程。通过解码技术直接对采样数据进行处理,从而达到重构原信号的目的。这就是压缩感知技术提出的动机。
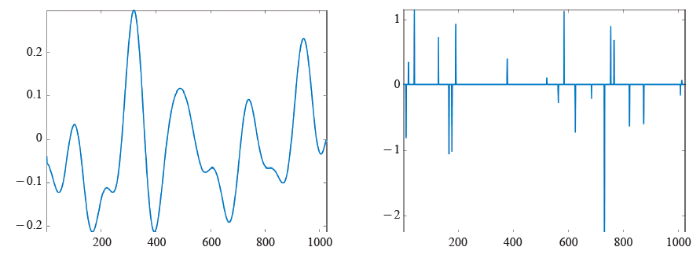
压缩感知 (compressive/compressed sensing/sampling) 是近年来兴起的信号处理技术,其奠基性理论工作由Candès、Rumberg和Tao[2]、Donoho[5]给出。压缩感知旨在克服传统信号处理理论中奈奎斯特采样率所造成的困难,并充分利用现实生活中的信号或图像通常具有稀疏性或可压缩性这一客观事实。与传统信号处理理论不同的是,压缩感知所假设的信号模型是稀疏性(sparse)与可压缩性(compressible)。称信号x是稀疏的,若其非零分量的个数远远小于其维数;称其是可压缩的,若其分量的绝对值从大到小快速衰减,或者等价的,它可由稀疏向量很好的近似。值得指出的是,稀疏性是一种趋势,而并非一个绝对的数值。当维数固定时,非零元的个数越少,信号就越稀疏。同样的,分量按绝对值从大到小衰减越快可压缩性就越好。绝大多数情况下,信号本身并不具有稀疏性或可压缩性。要获得稀疏性或可压缩性,需要考虑适当的正交变换Ψ,即s=ΨT x是稀疏或可压缩的。图2与图3分别给出了本身不稀疏,而在离散余弦变换下具有稀疏性或可压缩性信号的例子。
简单的说,压缩感知分为两步,即采样和重构。与传统采样不同的是,压缩感知的采样数据是信号x的各个分量的线性组合。因此,压缩感知的每一个采样数据均含有信号的某种整体信息。首先,压缩感知直接获取压缩了的采样数据y,这是硬件实现的过程,也称为编码。设采样数据y的维数为m,它与信号x的关系为y=Ax,这里A为m行n列的采样矩阵,也称为编码矩阵。之所以称y是压缩了的数据是因为m远远小于n。因此,压缩感知采样集传统信号处理中的采样与压缩于一体,既提高了采样的效率,又省去了变换编码的过程。其次,从数据y中重构信号x,也称为解码。在以下的讨论中,我们假设信号本身具有稀疏性或可压缩性,而不考虑正交变换Ψ。由于在理论上总可以用乘积矩阵AΨ代替采样矩阵A,这一假设是不失一般性的。压缩感知的两个重要要素是信号x具有稀疏性或可压缩性,并且采样矩阵A具有足够好的性质。采样矩阵需要满足一定的与稀疏或可压缩程度有关的条件才能在理论上保证通过适当的解码实现原信号的重构。因此,这两个要素紧密相关。
满足何种性质的采样矩阵是“好”的?一方面,在理论上完美的编码矩阵可能会给压缩感知第二阶段的解码过程造成难以克服的计算困难。另一方面,解码过程过于简单又会使得编码矩阵难以设计。因此,编码与解码两个方面必须结合起来考虑。简单的说,采样矩阵的选取应使得压缩了的采样数据Ax包含和原信号x同样多的信息,并且能够设计一种相对比较容易实现的解码器从压缩数据中重构原信号。解码器旨在从欠定系统Ax=y的解集中锁定原始信号。理论上,在没有任何先验条件的情况下,这是不可能实现的。然而,压缩感知理论的基本假设是原信号是稀疏的或可压缩的(可稀疏逼近)。一个自然的想法是寻找欠定系统Ax=y最稀疏的解来重构原信号。遗憾的是,这是一个极其困难的问题。事实上,它是NP难问题。因此,人们试图寻找上述最稀疏解的替代模型,如最小二模解、最小一模解等。人们长期的实践已经摸索出一个基本规律,即极小化一模通常能够得到稀疏解。早在1965年,Logan就将一模模型应用于消除信号离群数据上。使用一模模型解决应用问题兴起于1970年代,被用于寻找所谓的“sparse spike trains”。1986年,Santosa和Symes明确指出[10],使用极小化一模的准则在许多情况下能够非常有效地找到问题正确的解、稀疏的解。1990年代之后,关于一模的使用与研究就非常多了,产生了计算调和分析中著名的基追踪(Basis Pursuit)模型,统计中的LASSO模型等。2006年,Donoho论证了这一点[6]。我们在Matlab平台上运用如下代码
n=1000; m=300; p=30;
xs=zeros(n,1); rn=randperm(n); xs(rn(1:p))=randn(p,1);
A=randn(m,n); y=A*xs;
产生随机数据,并分别寻求欠定线性系统Ax=y的二模最小与一模最小的解。图4给出了实验结果。
可以看出,运用一模极小化的原则能够很准确地重构原信号,而二模极小化原则却不能。二模极小化原则找到的是能量最低的解,而非最稀疏的解。一模极小化则在很大程度上可以消除离群数据的影响,并锁定欠定线性系统最稀疏的解。限制在二维或三维空间时,这一区别具有很好的几何直观。压缩感知的基本理论回答了在何种情况下运用一模极小化原则可以以多大概率找到欠定线性系统最稀疏的解。
压缩感知的理论已经非常丰富,这里仅简要描述Candès、Rumberg和Tao在文献[2]中的奠基性工作。文献[2]证明了对于频率域的均匀采样,如果样本量m,信号x的维度n,以及x的非零元素个数p满足m≥Cplog(n),这里C>0为某常数,那么运用极小化一模的准则可以以极大的概率精确重构原信号。这一理论结果具有开创性的意义,奠定了压缩感知理论的基础。随后,这一结果得到广泛的推广,包括将采样矩阵推广到随机高斯矩阵、随机二进制矩阵、随机投影矩阵等,采样有噪声的情况,基于限制正交性(Restricted Isometry Property)的确定性分析,基于零空间性质(Null Space Property)的分析,不依赖于限制正交性的分析(Non-RIP analysis)等等。感兴趣的读者可参考Candès、Romberg和Tao的系列工作以及Donoho[5]、DeVore[4]和Zhang[13]等作者的文献。
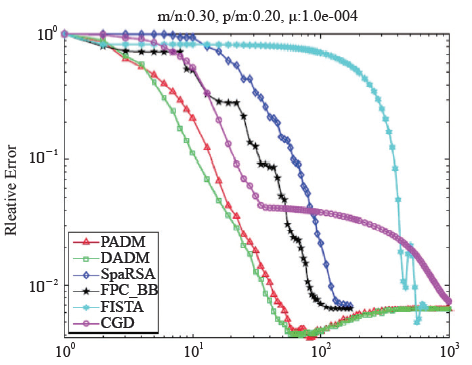
压缩感知的第二阶段为基于一模优化的解码。这里我们仅简要介绍一模优化与交替方向解码算法。感兴趣的读者可参考文献[11]。实际应用中,采样通常有误差。因此,对采样约束条件Ax=y进行松弛是合理的。此时,通常求解下面一模优化模型
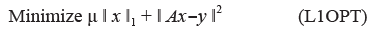
这里μ>0为正则化参数,它的大小与采样的噪声水平正相关。交替方向法提出于1970年代[7,8],它与最优化中著名的增广Lagrange乘子法、Douglas-Rachford算子分裂法、邻近点法都有着紧密的联系。其基本思想是分而治之、各个击破。首先,通过引入辅助变量将(L1OPT)等价变型,使目标函数具有可分结构。其次,利用增广Lagrange函数与交替极小化的技巧进行Gauss-Seidel类迭代计算,并及时更新乘子(对偶变量)。由于非光滑的一模函数与编码矩阵使得变量耦合带来的双重困难被分离到两个子问题中,并且子问题可以充分利用一模与二模平方函数的可分结构,算法的单步计算非常简单。事实上,当采样矩阵A的不同行互相正交时,可以设计算法使得每一子问题都有闭式解,算法单步计算量仅为两次矩阵向量乘法,且总体收敛速度快。对于更为一般的采样矩阵A,也可以对算法稍作修改以实现上述的算法简单与快速收敛。图5给出了交替方向算法(PADM与DADM)与其他解码算法在求解(L1OPT)模型时的数值比较结果,其中横轴代表迭代次数,纵轴代表相对误差,采样数据的噪声符合均值为0、标准差为10–3的高斯分布。图中结果为50次随机实验的平均。可以看出,交替方向算法与针对(L1OPT)特殊定制的SpaRSA,FPCBB, FISTA,CGD等算法相比,具有更快的收敛速度。
本文简略介绍了压缩感知理论、一模优化与交替方向解码。由于篇幅限制,未能展开介绍。关于压缩感知的中文综述文献可参考[14,15,16],更多资源可参考莱斯大学的网站[17]和博客[18]。目前,压缩感知的思想已被推广到矩阵完整化与鲁棒主成分分析,向量一范数相应的变成了矩阵核模(奇异值之和)。更为广泛的推广运用了atomic模的概念,可参考文献[3]。近几年,寻求问题的具有稀疏、结构稀疏、低秩等结构的解已得到广泛研究。交替方向法已被应用到数字图像与信号处理、高维数据分析、机器学习、分布式计算等诸多领域,感兴趣的读者可参考综述文献[1]。南京大学何炳生教授在交替方向法的理论与应用研究方面做出了突出贡献,参见文献[9]。最近,交替方向法的许多修改形式得到研究,如在线或随机形式的交替方向法,用以求解以大数据为背景的模型问题,算法单步计算量非常小,而与样本容量无关,并且算法总体收敛速度能够满足应用需求。此类方法已被应用到机器学习领域的支持向量机、逻辑回归等问题。可以预见交替方向相关的算法在未来将有越来越多的应用与发展。
致谢
感谢南京大学何炳生教授、莱斯大学张寅教授多年来给予的支持和帮助。本研究得到国家自然科学基金NSFC-11371192的支持。
The authors have declared that no competing interests exist.
| [1] |
|
| [2] |
|
| [3] |
DOI:10.1007/s10208-012-9135-7
Magsci
URL
[Cite within: 1]
In applications throughout science and engineering one is often faced with the challenge of solving an ill-posed inverse problem, where the number of available measurements is smaller than the dimension of the model to be estimated. However in many practical situations of interest, models are constrained structurally so that they only have a few degrees of freedom relative to their ambient dimension. This paper provides a general framework to convert notions of simplicity into convex penalty functions, resulting in convex optimization solutions to linear, underdetermined inverse problems. The class of simple models considered are those formed as the sum of a few atoms from some (possibly infinite) elementary atomic set; examples include well-studied cases such as sparse vectors and low-rank matrices, as well as several others including sums of a few permutations matrices, low-rank tensors, orthogonal matrices, and atomic measures. The convex programming formulation is based on minimizing the norm induced by the convex hull of the atomic set; this norm is referred to as the atomic norm. The facial structure of the atomic norm ball carries a number of favorable properties that are useful for recovering simple models, and an analysis of the underlying convex geometry provides sharp estimates of the number of generic measurements required for exact and robust recovery of models from partial information. These estimates are based on computing the Gaussian widths of tangent cones to the atomic norm ball. When the atomic set has algebraic structure the resulting optimization problems can be solved or approximated via semidefinite programming. The quality of these approximations affects the number of measurements required for recovery. Thus this work extends the catalog of simple models that can be recovered from limited linear information via tractable convex programming.
|
| [4] |
DOI:10.1117/12.725193
URL
[Cite within: 1]
The usual paradigm for signal processing is to model a signal as a bandlimited function and capture the signal by means of its time samples. The Shannon-Nyquist theory says that the sampling rate needs to be at least twice the bandwidth. For broadbanded signals, such high sampling rates may be impossible to implement in circuitry. Compressed Sensing is a new area of signal processing whose aim is to circumvent this dilemma by sampling signals closer to their information rate instead of their bandwidth. Rather than model the signal as bandlimited, Compressed Sensing, assumes the signal can be represented or approximated by a few suitably chosen terms from a basis expansion of the signal. It also enlarges the concept of sample to include the application of any linear functional applied to the signal. In this paper, we shall give a brief introduction to compressed sensing that centers on the effectiveness and implementation of random sampling.
|
| [5] |
|
| [6] |
DOI:10.1002/cpa.20132
URL
[Cite within: 1]
We consider linear equations y = Φα where y is a given vector in R n, Φ is a given n by m matrix with n < m ≤ An, and we wish to solve for α ∈ R m. We suppose that the columns of Φ are normalized to unit 61 2 norm 1 and we place uniform measure on such Φ. We prove the existence of ρ = ρ(A) so that for large n, and for all Φ’s except a negligible fraction, the following property holds: For every y having a representation y = Φα0 by a coefficient vector α0 ∈ R m with fewer than ρ · n nonzeros, the solution α1 of the 61 1 minimization problem min 17x171 subject to Φα = y is unique and equal to α0. In contrast, heuristic attempts to sparsely solve such systems – greedy algorithms and thresholding – perform poorly in this challenging setting. The techniques include the use of random proportional embeddings and almost-spherical sections in Banach space theory, and deviation bounds for the eigenvalues of random Wishart matrices.
|
| [7] |
|
| [8] |
DOI:10.1016/0898-1221(76)90003-1
URL
[Cite within: 1]
The approach is based on the use of an Augmented Lagrangian functional and leads to an efficient and simply implementable algorithm. We study also the finite element approximation of such problems, compatible with the use of our algorithm. The method is finally applied to solve several problems of continuum mechanics.
|
| [9] |
|
| [10] |
DOI:10.1137/0907087
URL
[Cite within: 1]
We present a method for the linear inversion (deconvolution) of band-limited reflection seismograms. A large convolution problem is first broken up into a sequence of smaller problems. Each small problem is then posed as an optimization problem to resolve the ambiguity presented by the band-limited nature of the data. A new cost functional is proposed that allows robust profile reconstruction in the presence of noise. An algorithm for minimizing the cost functional is described. We present numerical experiments which simulate data interpretation using this procedure.
|
| [11] |
DOI:10.1137/090777761
URL
[Cite within: 2]
In this paper, we propose and study the use of alternating direction algorithms for several $\ell_1$-norm minimization problems arising from sparse solution recovery in compressive sensing, including the basis pursuit problem, the basis-pursuit denoising problems of both unconstrained and constrained forms, as well as others. We present and investigate two classes of algorithms derived from either the primal or the dual forms of the $\ell_1$-problems. The construction of the algorithms consists of two main steps: (1) to reformulate an $\ell_1$-problem into one having partially separable objective functions by adding new variables and constraints; and (2) to apply an exact or inexact alternating direction method to the resulting problem. The derived alternating direction algorithms can be regarded as first-order primal-dual algorithms because both primal and dual variables are updated at each and every iteration. Convergence properties of these algorithms are established or restated when they already exist. Extensive numerical results in comparison with several state-of-the-art algorithms are given to demonstrate that the proposed algorithms are efficient, stable and robust. Moreover, we present numerical results to emphasize two practically important but perhaps overlooked points. One point is that algorithm speed should always be evaluated relative to appropriate solution accuracy; another is that whenever erroneous measurements possibly exist, the $\ell_1$-norm fidelity should be the fidelity of choice in compressive sensing.
|
| [12] |
|
| [13] |
|
| [14] |
DOI:10.3321/j.issn:0372-2112.2009.05.028
Magsci
URL
[Cite within: 1]
信号采样是联系模拟信源和数字信息的桥梁.人们对信息的巨量需求造成了信号采样、传输和存储的巨大压力.如何缓解这种压力又能有效提取承载在信号中的有用信息是信号与信息处理中急需解决的问题之一.近年国际上出现的压缩感知理论(Compressed Sensing,CS)为缓解这些压力提供了解决方法.本文综述了CS理论框架及关键技术问题,并着重介绍了信号稀疏变换、观测矩阵设计和重构算法三个方面的最新进展,评述了其中的公开问题,对研究中现存的难点问题进行了探讨,最后介绍了CS理论的应用领域.
|
| [15] |
DOI:10.3969/j.issn.1007-6093.2012.03.002
Magsci
URL
[Cite within: 1]
介绍压缩感知和稀疏优化的基本概念、理论基础和算法概要.压缩感知利用原始信号的稀疏性,从远少于信号元素个数的测量出发,通过求解稀疏优化问题来恢复完整的原始稀疏信号.通过一个小例子展示这一过程,并以此说明压缩感知和稀疏优化的基本理念.接着简要介绍用以保证l1,凸优化恢复稀疏信号的零空间性质和RIP条件.最后介绍求解稀疏优化的几个经典算法.
|
| [16] |
|
| [17] |
|
| [18] |
|